A decimal expansion is the most popular way to represent rational and irrational real numbers. It formalizes an idea you’re already probably aware of: fractions can be written as decimals.
A simple example: the fraction ½ could be represented by the decimal 0.5; So 0.5 is a decimal expansion of ½
More examples:
| Fraction | Decimal Expansion |
| 1/3 | .3 |
| 1/4 | .25 |
| 1/0 | .1 |
| 1/20 | .05 |
You can find a full list of decimal expansions for 1/b for values between 2 and 10 here. Another alternative: use a calculator. For example, typing in 1/7 into the Google calculator gives 0.14285714285.
Instead of writing out those numbers over and over again, we can write 0.142857, where the overline indicates a series of indefinitely repeating numbers.
Period of a Decimal Expansion
The period of a decimal expansion is the smallest block of repeating digits (if there are no repeating digits, the decimal is terminating).
Examples:
- The solution above repeats a block of 6 numbers 142857. This is called a repeating decimal because of the infinitely repeating digits. The period is 6.
- The number ½ can be expressed as a repeating decimal 0.3, which has a period of 1.
More Formal Definition
Any decimal expansion can be expressed as a base-10 geometric series. A geometric series can be written as:
a + ar + ar2 + ar3 + …
Where:
- a is the initial term,
- r is the common ratio.
Example question: Express the decimal expansion 0.121212… as a geometric series.
Step 1: Split the decimal into its repeating parts:
0.121212… = 0.12 + 0.0012 + 0.000012…
Step 2: Rewrite the parts from Step 1 as fractions:
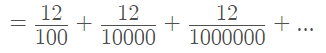
Step 3: Find the common ratio. Each of the above terms can be found by multiplying by the common ratio of 1/100:
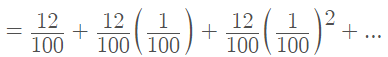
Which means this geometric series has:
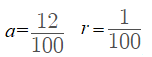
The sum of this geometric series tells us that the fraction (4/33) has a decimal expansion of 0.121212…
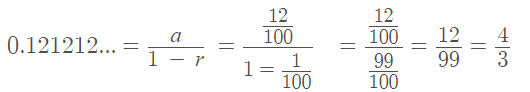
References
Comez, D. (2016). Decimal Expansion Representation of Real Numbers. Retrieved April 21, 2021 from: https://www.ndsu.edu/pubweb/~comez/Decimal%20expansion.pdf