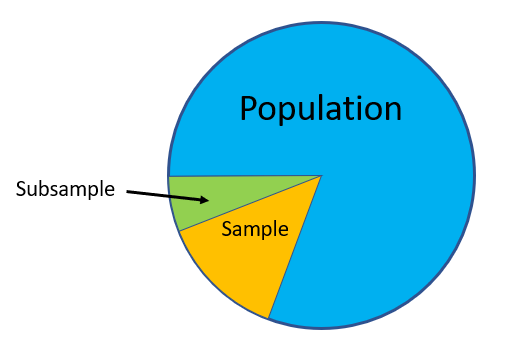
In statistics, a subsample is a sample of a sample. In other words, a sample is part of a population and a subsample is a part of a sample.
For example, let’s say you had a population of one million people, and you used simple random sampling to get a sample of 1,000 people. You could use simple random sampling again on the 1,000 people to get a smaller portion of 100 people.
Why Subsample?
One reason is to fairly and equally divide a sample for further analysis. For example, let’s say you were conducting a survey on a sample of 1,000 people with 10 interviewers. You suspect that interviewers may bring their own biases to the interview, so you decide to divide the sample randomly into 10 different subsamples, each with 100 people for each interviewer.
Subsampling vs. Resampling and Sample Splitting
Sample splitting is where data is split into half. One half of the data is fit to a penalized regression model (with lasso regression or similar) and the remaining half of the data is fit to ordinary least squares. One disadvantage compared to subsampling is lower statistical power and uncertain results, which vary depending on which split is chosen for analysis [1].
While subsampling can be performed once, all resampling methods are usually performed multiple times using the same procedure, like bootstrap, cross validation, or Jackknife [2, 3]. This isn’t a hard and fast rule: sometimes subsampling is used as a synonym for bootstrapping [4]. Resampling can be done with replacement, or without replacement.
References
[1] Breheny, P. (2013). Inference: Subsampling and Resampling Approaches. Retrieved November 27, 2021 from: https://myweb.uiowa.edu/pbreheny/7600/s16/notes/4-13.pdf
[2] McLapham, M. Resampling methods. Retrieved November 27, 2021 from: https://websites.pmc.ucsc.edu/~mclapham/Rtips/resampling
[3] Computational Statistics in Python.
[4] Geyer, C. (2013). The Subsampling Bootstrap. Retrieved November 27, 2021 from: https://www.stat.umn.edu/geyer/5601/notes/sub.pdf