A saddle point (or minimax point) on a graph of a function, is a critical point that isn’t a local extremum (i.e., it’s not a local maximum or a local minimum).
Another way of stating the definition is that it is a point where the slopes (or derivatives) in orthogonal directions are all zero. However, the point is not the highest or lowest point in its neighborhood.
Imagine the graph of a function which was shaped like a saddle, or like two mountains connected by a mountain pass. Then the saddle point would be at the center of the seat, hence the name. Take a step in one direction, and you are going on an upward curve; take a step in another direction, and you are on a downward curve, but right at the saddle point the slope is zero.
Below, the saddle point is marked in red on the graph of x2 – y2. Notice this point is right at the origin.
It is a stationary point, and the curve or surface in its neighborhood is not entirely on any side of its tangent space.
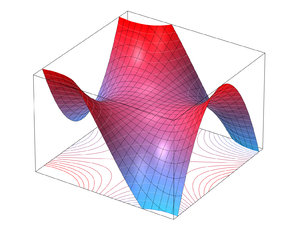
Multiple Saddle Point Surfaces
A smooth surface which has one or more saddle points is called a saddle surface. The graph above would be an example of a saddle surface; as would a Pringles potato chip or the form of an ordinary saddle.
A classic three dimensional saddle surface is the monkey saddle, defined by z = x3 -3xy2 and pictured below. If the name seems a bit random, try imagining it as a saddle for a monkey, with a place for both legs and another place for the tail.
References
Kiffe, Tom. A Saddle Point. Calculus Visualizations. Calculus 3 Course Material. Retrieved from http://www.math.tamu.edu/~tom.kiffe/calc3/saddle/saddle.html on March 7, 2019