Pearson Correlation Coefficient > Restricted Range
What is a Restricted Range?
A restricted range is a range of values that has been condensed, or shortened. For example, the entire range of G.P.A. scores is 0 to 4.0. A restricted range could be 3.0 to 4.0, or 2.0 to 3.0.
Restricted Range and Correlation
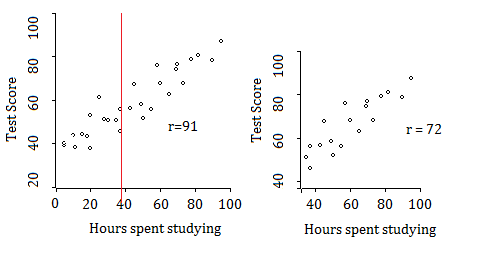
Restricted ranges affect correlations. In fact, when the range is restricted, a peculiar phenomenon happens: the correlation coefficient goes down. The following image shows the correlation between hours studying and test scores. Not surprisingly, the correlation coefficient is rather high: 0.91. However, when the range is restricted to people who studied more (about 40 hours — to the right of the red line), the correlation coefficient goes down — to 0.72.
For this particular example, restricting the range to the left of the red line would reduce the correlation coefficient even further, to 0.50:
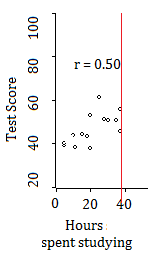
Although there is a very strong correlation overall (.91), this association is weakened to 0.72 and 0.50 when the range is split into two.
Therefore, if you’re dealing with a restricted range and the correlation coefficient is small (or zero), you shouldn’t draw the conclusion that there isn’t a correlation. Your results may simply be a product of this peculiar phenomenon.
Real Life Example
In a study of diabetic patients, Bland & Altman (2011) found a strong correlation (r = 0.85) between waist measurement and BMI. However, the correlation differed for varying restricted ranges. When the range was restricted to BMIs over 35, the correlation coefficient was 0.86. For BMIs between 30 and 35, there was practically no correlation (-0.09). The overall trend, however, was for the correlation coefficient to become smaller for restricted ranges.
| BMI Group | Correlation Coefficient (r) |
| <25 | 0.62 |
| 25 to 30 | 0.50 |
| 30 to 35 | -0.09 |
| > 35 | 0.86 |
| All patients | 0.85 |
References
Bland, J. & Altman, D. (2011). Correlation in restricted ranges of data. BMJ 2011; 342 doi: https://doi.org/10.1136/bmj.d556 (Published 11 March).
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.