The range rule of thumb is a handy method of estimating the range from the standard deviation. It tells us that the range is generally about four times the standard deviation.
So if your standard deviation is 2, you might guess that your range is about eight.
Using the range rule of thumb it is also possible to estimate a standard deviation when you know the range. Simply divide the range by four.
The range rule of thumb works best for data from a normal distribution where the sample size is close to thirty. For samples that are either much smaller or much larger than thirty, or do not follow the normal distribution, it can be a very bad guess.
Alternate Rules
There are alternative ‘rules of thumb’ which tend to provide better guesses, but they are also much heavier on calculation. For example, one suggestion from Ramirez and Cox (2012) for a rule is as follows:
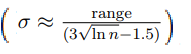
The formula is limited to the normal distribution, but the authors do offer suggestions for other distributions.
Other Uses of the Range Rule of Thumb
The range rule of thumb suggests that most values would be in the area covered by four standard deviations: i.e., within two standard deviations above or below the mean. This allows us to define unusual values as those which don’t fall into this range. We call the maximum usual value the mean plus two standard deviations, and the minimum usual value the mean minus two standard deviations.
References
Ramirez, Alfredo. Cox, Charles. Improving on the Range Rule of Thumb. Rose Hulman Undergraduate Mathematics Journal, Volume 13, No. 2, Fall 2012. Retrieved from https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1211&context=rhumj on August 28, 2018.
Triola, M.F. Elementary Statistics Using Excel. Section 5-2, Random Variables. Retrieved from http://math.tntech.edu/e-stat/TRIOLA/Chapter5.pdf on August 28, 2018.
Jones, James. Measures of Variance. Retrieved from https://people.richland.edu/james/ictcm/2001/descriptive/helpvariance.html on August 28, 2018.
Tanbakuchi, Anthony. Introductory Statistics Lectures: Measures of Variation. Department of Mathematics, Pima Community College. Retrieved from http://www.u.arizona.edu/~kuchi/Courses/MAT167/Files/LH_LEC.0230.DescStats.Variation.pdf on August 28, 2018.