Pi Derivative & Derivative of Circle’s Area

Common Derivatives > Pi Derivative

The derivative of π with respect to x is 0.

π is a constant (equal to about 3.14), and the derivative of a constant is zero. Therefore π², π/2, π/6, π/10 or any other π/constant variants all have derivatives of zero.

This only works if you have a constant. It doesn’t work if you have any variable in your expression. For example, the rule doesn’t apply to π(x), π²(x) or πsin(x).

There are some other interesting relationships with derivatives involving π, especially the one involving the derivative of the area of a circle.

Pi Derivative in Other Functions

Examples:

1. π²(x)
2. x^π
3. π^x

Example #1 : What is the derivative with respect to x of
f(x) = π²(x)?

Step 1: Place the constant in front:
= π^{2 d}/_dx(x).

Step 2: Use the common pi derivative ^d/_dx = 1:
= π² · 1.

Step 3: Simplify:
= π².

Example #2 : What is the derivative with respect to x of
f(x) = x^π?

Step 1: Use the power rule ^d/_dx (x^a = a · x^{a – 1}):
We have a = π so:
= πx^π-1

That’s it!

Example #3 : What is the derivative with respect to x of f(x) = π^x?

Step 1: Use the common derivative rule for exponential functions ^d/_dx(a^x = a^xln(a)):
Plugging our function into the formula, we have a = π, so:
= π^xln(π).

These examples demonstrate that we can use common rules to simplify functions involving a pi derivative.

Derivative of a Circle’s area πr²

The derivative of a circle’s area (πr²) is it’s circumference (2*πr).
This relationship also holds for a semicircle, and it can be extended to a sphere: the derivative of the volume function of a sphere equals its surface area. This interesting derivative relationship does not hold for all shapes though, such as squares or rectangles [1].

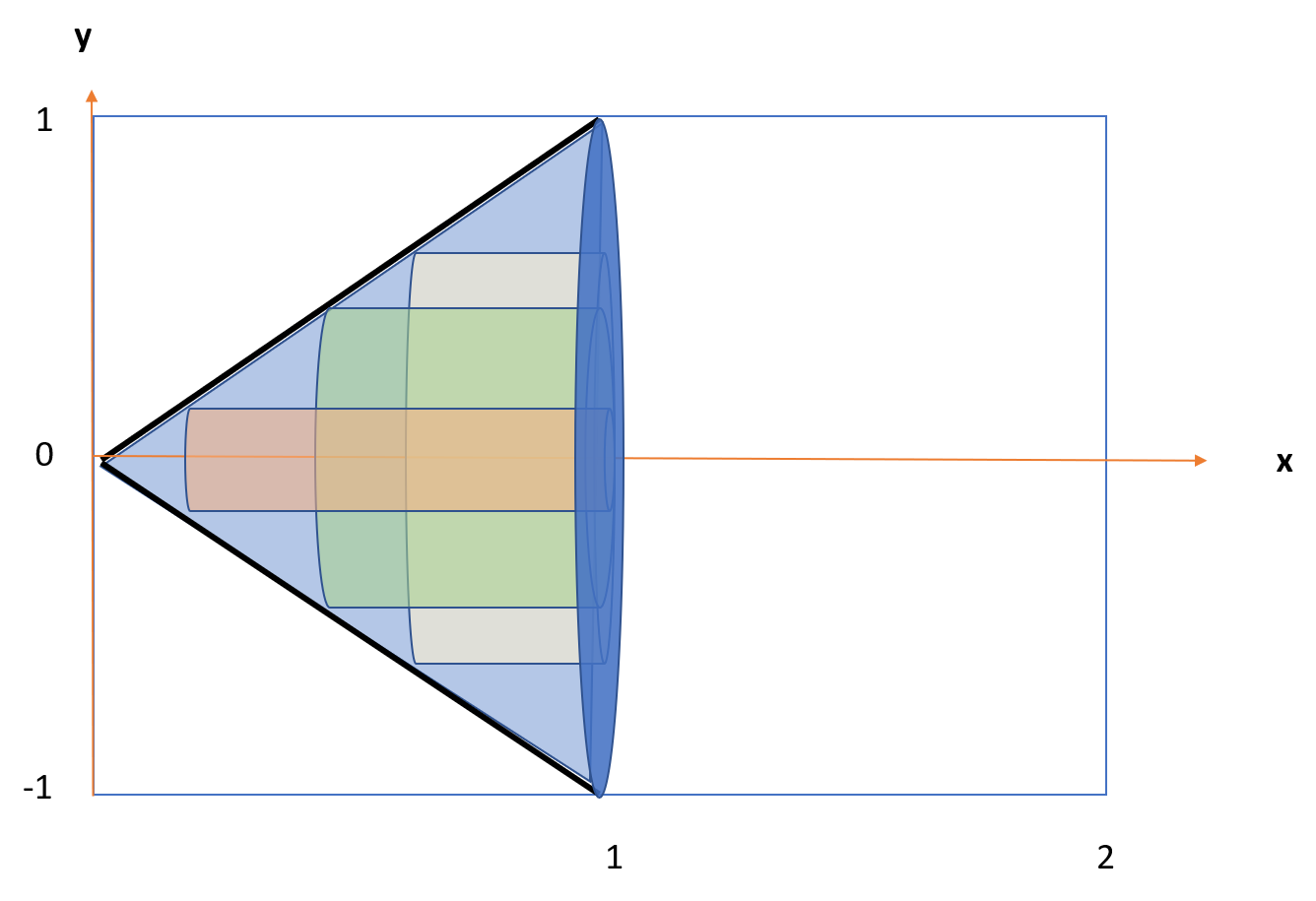
The math behind this fact is used in the cylindrical shell method for finding volumes of shapes. The logic is as follows [2]: a small change in the radius of the sphere produces a small change in the sphere’s volume, which is equal to the volume of a spherical shell of radius R and thickness δR. This shell’s volume is approximately:
V = Surface area of sphere * δ R.
The derivative here is the change in ball volume / δR, which is just the surface area of the sphere.

Pi Derivative: References

[1] Marichal, J. & Dorff, M. (2007). Derivative Relationships between volume and surface area of compact regions in R^d. Rocky Mountain Journal of Mathematics, vol 37 No 2. Retrieved May 3, 2021 from: https://math.byu.edu/~mdorff/docs/SomeRelations2007.pdf
[2] Su, Francis E., et al. “Surface Area of a Sphere.” Math Fun Facts. .