Parsimonious Model: Definition, Ways to Compare Models

Regression Analysis > Parsimonious Model

What is a Parsimonious Model?

Parsimonious models are simple models with great explanatory predictive power. They explain data with a minimum number of parameters, or predictor variables.

The idea behind parsimonious models stems from Occam’s razor, or “the law of briefness” (sometimes called lex parsimoniae in Latin). The law states that you should use no more “things” than necessary; In the case of parsimonious models, those “things” are parameters. Parsimonious models have optimal parsimony, or just the right amount of predictors needed to explain the model well.

Comparing Models

There is generally a tradeoff between goodness of fit and parsimony: low parsimony models (i.e. models with many parameters) tend to have a better fit than high parsimony models. This is not usually a good thing; adding more parameters usually results in a good model fit for the data at hand, but that same model will likely be useless for predicting other data sets.

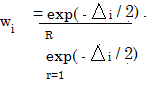
Finding the right balance between parsimony and goodness of fit can be challenging. Popular methods include Akaike’s Information Criterion (AIC), Bayesian Information Criterion (BIC), Bayes Factors and Minimum Description Length.

Akaike’s Information Criterion compares the quality of a set of models; The AIC will rank each option from best to worst. The most parsimonious model will be the one that neither under-fits nor over-fits. One downside is that the AIC says nothing about quality; If you input a series of poor models, the AIC will choose the best from that poor-quality set.
The Bayesian Information Criterion (BIC) is almost the same as the AIC, although it tends to favor models with fewer parameters. The BIC is also known as the Schwarz information criterion or Schwarz’s BIC.
Bayes Factors compare models using prior distributions. It is similar to the Likelihood Ratio Test, but models do not have to be nested. Model selection based on Bayes Factors can be approximately equal to BIC model selection. However, BIC doesn’t require knowledge of priors so it is often preferred.
Minimum Description Length (MDL): commonly used in computer and information science, it works on the basis that strings of related data can be compressed, reducing the number of predictor variables.