A canonical statistic (sometimes called a natural statistic) is a way to specify a particular exponential distribution. All exponential families of distributions over x have the general form (Creager, 2018)
p(x| η) = h(x) g(η) exp{ηT u(x)}
Where:
- u(x) is the canonical (natural) statistic, which is a function of x,
- η is the natural parameter,
- h(x) is the base measurement, which is often constant,
- g(η) is the normalizer.
The canonical statistic is usually a minimal sufficient statistic.
Example:
A sequence of Bernoulli trials might result in the following probability function for the outcome sequence y = (y1, … yn (Sundberg, 2019):
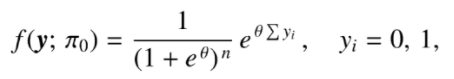
The canonical statistic here is y(y) = Σ yi (Σ is summation notation, which means to “Add them up”).
Non Uniqueness of a Canonical Statistic
The name “canonical” in math means to indicate a choice from a particular number of different conventions, leading to a unique choice. However, a canonical parameter and statistic are not unique (Geyer, 2020):
- Any one-to-one affine function of a canonical parameter (or statistic) is canonical. However, these change the canonical statistic (or parameter) in addition to the cumulant function.
- A scalar-valued affine function of the canonical parameter can be added to the cumulant function. This will change the canonical statistic.
Although there are many possibilities, the workaround is to make a choice: “The” canonical statistic is a result of fixing one choice of statistic, from all of the different possibilities.
Related article: Canonical Correlation Analysis / Variates.
References
Creager, E. (2018). Introduction to Advanced Probability for Graphical Models. Retrieved January 15, 2021 from: http://www.cs.toronto.edu/~jessebett/CSC412/content/week1/tutorial1-probability-412–ec-edit.pdf
Geyer, C. (2020). Stat 5421 Lecture Notes. Exponential Families, Part I.
Sundberg, R. (2019). Statistical Modelling by Exponential Families. Cambridge University Press.