The general Leibniz rule is an extension of the product rule to higher order derivatives. More specifically, this rule for repeated differentiation expresses the nth derivative of a product fg in terms of the product of derivatives. It is given by the formula:
![]()
If this looks vaguely familiar, that might be because the general Leibniz rule is a generalization of the product rule—which is sometimes called the “Leibniz rule”.
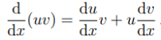
More technically speaking, the general Leibniz rule is another way to express partial derivatives of a product of functions — as a linear combination of terms involving the functions’ products of partial derivatives (Brummer, 2000).
A Closer Look at the General Leibniz Formula
Like many rules in calculus, there are various ways the formula can be written. For example, the rule may be written in summation notation as:
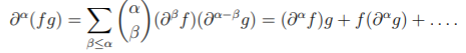
Where:
- ∂ = “Curly d” notation for partial derivatives (used in place of the derivative “d” for functions of more than one variable),
- f and g are two real-valued, differentiable functions and
- The multi-index α is a non-negative integer.
Like the simpler product rule, there are two terms on the right-hand side. One of the terms has all α derivatives on f and zero derivatives on g; The other term has zero derivatives on f and all α derivatives on g.
The formula gives rise to a host of Leibniz type rules, including fractional Leibniz rules (Brummer, 2018). The rule can easily be extended to multiple products by switching out the binomial coefficient. For example, triple products can be evaluated with a trinomial coefficient.
References
Brummer, J. Research Statement. Retrieved September 18, 2020 from:https://www.math.ksu.edu/~brummerjd/Brummer_ResearchStatement.pdf
Brummer, J. (2018). Leibniz-type rules associated to bilinear pseudodifferential operators. Dissertation abstract. Retrieved September 18, 2020 from: https://krex.k-state.edu/dspace/bitstream/handle/2097/39030/JoshuaBrummer2018.pdf?sequence=3
Changala, B. (2018). NITROGEN Reference Guide. Retrieved September 18, 2020 from: https://www.colorado.edu/nitrogen/sites/default/files/attached-files/usermanual_0.pdf
Szpruch, L. V-stable tamed Euler Spaces. Retrieved September 18, 2020 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.740.6626&rep=rep1&type=pdf