What is Explicit Differentiation?
Explicit Differentiation is taking the derivative of an explicit function.
What is an “Explicit Function”?
In an explicit function, one variable is defined completely in terms of the other. This usually means that the independent variable (x) is written explicitly in terms of the dependent variable (y). The general form is: y = f(x). Note that “y” is on one side of the equals sign and “x” is on the other side.
Most of the functions you’re probably familiar with are explicit, like y = x2 or y = 2x + 3. When you first start in calculus, practically all of the functions you work with are going to be in this explicit form, and you’ll use the usual rules for differentiation.
What is “Implicit”?
The opposite of an explicit function is an implicit function, where the variables become a little more muddled. For example, the following equations are implicit:
- x2 + y2 = 1 (x and y are on one side of the equation)
- y*ey = x (two “y”s are on one side of the equation).
Explicit Differentiation vs. Implicit Differentiation
When you have a function that’s in a form like the above examples, it isn’t possible to use the usual rules of differentiation. When that’s the case, you have two choices:
- Rewrite the equation so that one variable is on each side of the equals sign, then differentiate using the normal rules.
- Use implicit differentiation.
Sometimes, the choice is fairly clear. For example, if you have the implicit function x + y = 2, you can easily rearrange it, using algebra, to become explicit: y = f(x) = -x + 2. In other cases, it might be easier to just use implicit differentiation.
Example
Let’s say you wanted to differentiate the implicit function x4 + 2y2 = 4.
1. Using explicit differentiation:
Rewrite, using algebra, so that you have one variable on each side of the equals sign:
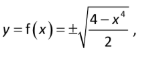
This would give you two derivatives, one for positive values of y, and one for negative values of y.
2. Using implicit differentiation:
Instead of rewriting, you can just go ahead and plug the function in:
![]()