Matrices > Correlation Matrix
You may find it helpful to read this article first: What is Pearson’s Correlation Coefficient?
What is a Correlation Matrix?
A correlation matrix is a table showing correlation coefficients between sets of variables. Each random variable (Xi) in the table is correlated with each of the other values in the table (Xj). This allows you to see which pairs have the highest correlation.
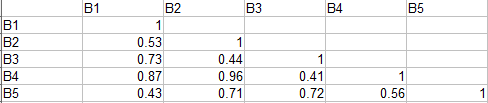
The diagonal of the table is always a set of ones, because the correlation between a variable and itself is always 1. You could fill in the upper-right triangle, but these would be a repeat of the lower-left triangle (because B1:B2 is the same as B2:B1); In other words, a correlation matrix is also a symmetric matrix.
What Kind of Data Can I Compare?
The correlation matrix is simply a table of correlations. The most common correlation coefficient is Pearson’s correlation coefficient, which compares two interval variables or ratio variables. But there are many others, depending on the type of data you want to correlate. The following table shows some of the common choices for correlation coefficients:
| Quantitative | Ordinal | Nominal | |
| Quantitative | Pearson | Biserial | Point Biserial |
| Ordinal | Biserial | Spearman rho/Tetrachoric | Rank Biserial |
| Nominal | Point Biserial | Rank Biserial | Phi, Goodman & Kruskal’s Lambda |
APA Formatting
If you include a correlation matrix in your research paper, your matrix should be treated as a table. You’ll want to follow some basic guidelines to formatting tables per APA rules.
The following image shows the basic structure of a correlation matrix, formatted as a table for APA:

Some general tips for formatting correlation matrices in APA Style:
- The title should be clear and explain the table contents. For example: Correlation matrix showing Pearson’s r for income and health data.
- Headings should be clear and brief. Keep them to one or two words (ideally no wider than a column width). All columns must have headings.
- Keep decimal places consistent (e.g. two places).
See also: reporting statistics APA style.
For full instructions on how to format tables in general, see the Owl at Purdue guide to formatting tables, APA style.
References:
Owl at Purdue