Confidence Intervals > Clopper-Pearson
The Clopper-Pearson interval, also called the exact interval is an alternative to calculating binomial confidence intervals using normal approximation. It is based on inverting the equal-tailed binomial tests. It is the most commonly cited exact method for finding a confidence interval [1].
The Clopper-Pearson exact method is strictly conservative and therefore considered to be exact. As the method is conservative, it may not give the shortest possible interval containing the desired confidence interval [2]. This is especially true when you know the population size. Although the Clopper-Pearson exact method was intended to have a minimum coverage of 95% [3], in the majority of cases the coverage can exceed 99%.
Clopper-Pearson Exact Method Formula
The formula for the Clopper-Pearson exact method uses the relationship between the Binomial distribution and Beta distribution to form the interval.
The formula for the Clopper-Pearson interval is [2]:
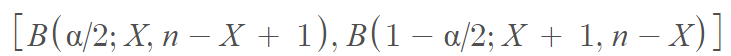
where B(·; α, β) is the beta distribution quantile function with shape parameters α and β.
Given an observation , the lower P and upper limits are given by [4]:
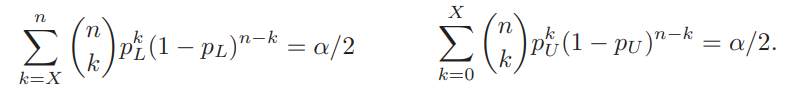
References
[1] Szekely, G. et al. [Eds.] (2000). Statistics for the 21st Century. Taylor & Francis.
[2] Helwig, N. (2020). Inference for proportions. Retrieved May 28, 2021 from: http://users.stat.umn.edu/~helwig/notes/ProportionTests.pdf
[3] Clopper,C.J.,and Pearson,E.S.(1934),“The Use of Confidence or Fiducial Limits Illustrated in the Case of the Binomial”, Biometrika 26, 404–413.
[4] Thulin, M. (2014). The cost of using exact confidence
intervals for a binomial proportion. Electronic Journal of Statistics. Vol 8. 817-840.