Bilinear regression is an informal term (i.e. there is no set definition for its meaning). Therefore, it might mean something different depending on who is using the term and in what context.
General Class of Regressions
One way to define bilinear regression is as a membership to the class of regressions on estimated latent variables. Latent variables are “hidden” variables that, unlike observed variables, are not directly measurable. Examples of latent variables include attitude, intelligence or degree of empathy. The two major bilinear regression methods in this context are principal component regression and partial least squares regression.
Bilinear Regression and Bilinear interactions
One of the most common definitions for bilinear regression is in terms of bilinear interactions. A bilinear interaction is where the slope of a regression line for Y and X changes as a linear function of a third variable, Z.
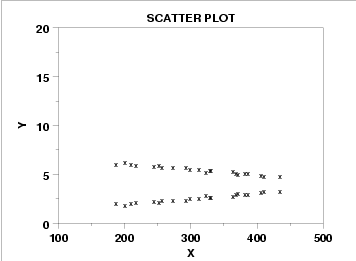
The simple act of creating two separate linear regressions is sometimes called bilinear regression. When a latent variable causes a scatter plot to have two distinct lines (as in the above image), two separate linear regressions might be warranted (one for each line).
In terms of matrices, bilinear regression can refer to a set of explanatory variables that form a two-dimensional matrix.
Generalized Bilinear Model
The generalized bilinear model1 can be written as: g(μij ) = α1iβ1j + α2iβ2j. Two specific models are the growth curve model and the extended growth model.
References:
R-project. Introduction to Generalized Linear Models.
Marie Linder, Rolf Sundberg. Precision of Prediction in Second Order Calibration, with Focus on BR Methods. Mathematical Statistics, Stockholm University, SE-106 91 Stockholm, Sweden. Retrieved July 26, 2017 from: http://staff.math.su.se/rolfs/Publikationer/Oct00.pdf