What is an Asymptotic Test?
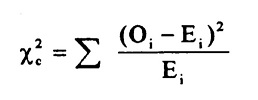
In hypothesis testing, you generally have two choices: an exact test or an asymptotic test. You can think of an asymptotic test as an approximation and an exact test as “the exact result.” For example, the chi-square test is an asymptotic test; the exact version is the binomial test, which creates approximations for p-values. The more data points you have, the better the asymptotic test approximation. However, large samples come with a computational cost—you may simply not have enough computer resources to be able to run one. In that case, an exact test might be the better option.
As a specific example, Let’s say you wanted to test marginal homogeneity with a sample size of 6. The usual test to run is the asymptotic McNemar’s test. However, the small sample means you can’t use the asymptotic version of McNemars test; Instead, you can use the exact version, which uses binomial probabilities [1].
Why Use Asymptotic Test Statistics?
Sometimes it isn’t possible to calculate exact statistics for a test due to hardware of software constraints. Instead, we can calculate an approximation of the “true” statistic, an asymptotic test value. Many statistical tests used asymptotic test values, especially for large samples. For example, you might see a p-value reported as .001 when in fact the exact p-value might have dozens of decimal places.
It is computationally efficient to give these approximations and it usually makes no difference to the results of a statistical test. However, for small samples or sparse data, exact values are usually recommended as approximations can be significantly different than the true values.
References
[1] Park, T. Is the exact test better than the asymptotic test for testing marginal homogeneity? Retrieved November 17, 2021 from: https://www.stat.fi/isi99/proceedings/arkisto/varasto/park0373.pdf