Additive Model and Multiplicative Model in Regression
The additive model and multiplicative model are generalizations of the “usual” linear regression model (Hastie & Tibshirani, 1990).
The additive model is the arithmetic sum of the predictor variables‘ individual effects. For a two factor experiment (X, Y), the additive model can be represented by:
Y = B0 + B1 X1 + B2 X2 + ε
Similarly, a multiplicative model can be represented by:
Y = B0 * B1 X1 * B2 X2 + ε
Their advantage is that they are more flexible than linear models, but keep many of the desirable properties of their linear counterparts (Shalizi, 2015). However, the models have issues with model selection, overfitting, and multicollinearity.
Additive and Multiplicative Model in Time Series
The terms can also refer to a particular model for time series data, where the model can be decomposed into four different components, related in an additive sense. For example, the model can be represented by:
yt = Tt + St + Ct + Rt
In summation (sigma) notation, the additive model can be represented, equivalently, by:
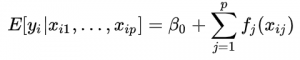
Or
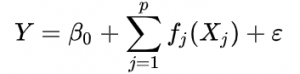
If the components are related instead by multiplication, the model is a multiplicative model:
yt = Tt * St * Ct * Rt
The multiplicative model is generally thought to be more accurate than the additive model (Fleming & Nellis, 2000).
References
Fleming, M. & Nellis, J. (2000). Principles of Applied Statistics: An Integrated Approach Using MINITAB and Excel. Thomson Learning.
Hastie, T. & Tibshirani, R. (1990). Generalized Additive Models. Chapman and Hall/CRC
Shalizi, C. (2015). Chapter 9: Additive Models. Retrieved August 3, 2020 from: https://www.stat.cmu.edu/~cshalizi/uADA/15/lectures/10.pdf
Tibshirani, R. (2014). Additive Models. Advanced Methods for Data Analysis (36-402/36-608). Retrieved August 3, 2020 from: https://www.stat.cmu.edu/~ryantibs/advmethods/notes/addmodels.pdf