Conditional probability is the probability of one event occurring with some relationship to one or more other events.
Events in Conditional Probability
Conditional probability could describe an event like:
- Event A is that it is raining outside, and it has a 0.3 (30%) chance of raining today.
- Event B is that you will need to go outside, and that has a probability of 0.5 (50%).
A conditional probability would look at these two events in relationship with one another, such as the probability that it is both raining and you will need to go outside.
The formula for conditional probability is:
P(B|A) = P(A and B) / P(A)
which you can also rewrite as:
P(B|A) = P(A∩B) / P(A)
Need help with homework? Check out our tutoring page!
Conditional Probability Formula Examples
Example 1
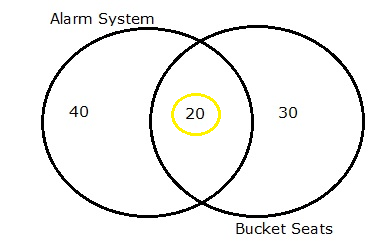
In a group of 100 sports car buyers, 40 bought alarm systems, 30 purchased bucket seats, and 20 purchased an alarm system and bucket seats. If a car buyer chosen at random bought an alarm system, what is the probability they also bought bucket seats?
Step 1: Figure out P(A). It’s given in the question as 40%, or 0.4.
Step 2: Figure out P(A∩B). This is the intersection of A and B: both happening together. It’s given in the question 20 out of 100 buyers, or 0.2.
Step 3: Insert your answers into the formula:
P(B|A) = P(A∩B) / P(A) = 0.2 / 0.4 = 0.5.
The probability that a buyer bought bucket seats, given that they purchased an alarm system, is 50%.
Example 2:
This question uses the following contingency table:

What is the probability a randomly selected person is male, given that they own a pet?
Step 1: Repopulate the formula with new variables so that it makes sense for the question (optional, but it helps to clarify what you’re looking for). I’m going to say M is for male and PO stands for pet owner, so the formula becomes:
P(M|PO) = P(M∩PO) / P(PO)
Step 2: Figure out P(M∩PO) from the table. The intersection of male/pets (the intersection on the table of these two factors) is 0.41.

Step 3: Figure out P(PO) from the table. From the total column, 86% (0.86) of respondents had a pet.

Step 4: Insert your values into the formula:
P(M|PO) = P(M∩PO) / P(M) = 0.41 / 0.86 = 0.477, or 47.7%.
Why do we care about conditional probability? Events in life rarely have simple probability. Think about the probability of getting rainfall.

Conditional Probability in Real Life
Conditional probability is used in many areas, in fields as diverse as calculus, insurance, and politics. For example, the re-election of a president depends upon the voting preference of voters and perhaps the success of television advertising—even the probability of the opponent making gaffes during debates!
The weatherman might state that your area has a probability of rain of 40 percent. However, this fact is conditional on many things, such as the probability of…
- …a cold front coming to your area.
- …rain clouds forming.
- …another front pushing the rain clouds away.
We say that the conditional probability of rain occurring depends on all the above events.
More Conditional Probability Real Life Examples
- Imagine that you’re a furniture salesman. The probability of a new customer to your store purchasing a couch on any particular day is 30%. However, if they are entering your store in the month leading up to the Super Bowl, the probability might be 70%. We can represent the conditional probability of selling a couch if it is the month leading up to Super Bowl as P(Selling a couch | Super Bowl month) where the | symbol means “given that”. This conditional probability gives us a way to express probabilities when our beliefs change about the probability of one event happens (a couch sale in this example) given that a certain event has happened (in this case, the advent of the month preceding the Super Bowl).
- The probability of a woman between 40 and 50 years of having breast cancer is about 1%. However, this probability changes if a woman has a positive mammogram: the probability a woman has cancer if she has a positive mammogram result rises to about 8.3% [1].
- Four candidates A, B, C, and D are running for a political office. Each has an equal chance of winning: 25%. However, if candidate A drops out of the race due to ill health, the probability will change: P(Win | One candidate drops out) = 33.33%.
- If you’re pregnant, the probability of having a boy or girl is the same: 50%. However, if you already have one child (say, a boy), your odds change. Given that your first child is a boy, your odds of having another boy drop to one third (33.33%). The reason for this is that the sample space for the event you have one boy out of two is S = {BB, BG, GB}. If you have one boy, the only possible event within this space is BB, which is one third of the sample space [2].
Where does the Conditional Probability Formula Come From?
The formula for conditional probability is derived from the probability multiplication rule, P(A and B) = P(A)*P(B|A).
Step by step, here’s how to derive the conditional probability equation from the multiplication rule:
Step 1: Write out the multiplication rule:
P(A and B) = P(A)*P(B|A)
Step 2: Divide both sides of the equation by P(A):
P(A and B) / P(A) = P(A)*P(B|A) / / P(A)
Step 3: Cancel P(A) on the right side of the equation:
P(A and B) / P(A) = P(B|A)
Step 4: Rewrite the equation:
P(B|A) = P(A and B) / P(A)
Check out our YouTube channel for more stats help and tips!
References
[1] Bayes’ Formula. Article posted on Cornell University website.
[2] Mitchell, J. Examples: Conditional Probability. Retrieved November 8, 2021 from: http://www.ams.sunysb.edu/~jsbm/courses/311/conditioning.pdf
Behara, R. Probability Quick Study Reference Outline. BarCharts; Lam Rfc Cr edition. 2010.