In order to follow this article, you may want to read these articles first:
What is a Hypothesis Test?
What are Type I and Type II Errors?
What is Power?
Watch the video for a brief overview of power.
The statistical power of a study (sometimes called sensitivity) is how likely the study is to distinguish an actual effect from one of chance. It’s the likelihood that the test is correctly rejecting the null hypothesis (i.e. “proving” your hypothesis). For example, a study that has an 80% power means that the study has an 80% chance of the test having significant results.
- A high statistical power means that the test results are likely valid. As the power increases, the probability of making a Type II error decreases.
- A low statistical power means that the test results are questionable.
Statistical power helps you to determine if your sample size is large enough.
It is possible to perform a hypothesis test without calculating the statistical power. If your sample size is too small, your results may be inconclusive when they may have been conclusive if you had a large enough sample.
Statistical Power and Beta
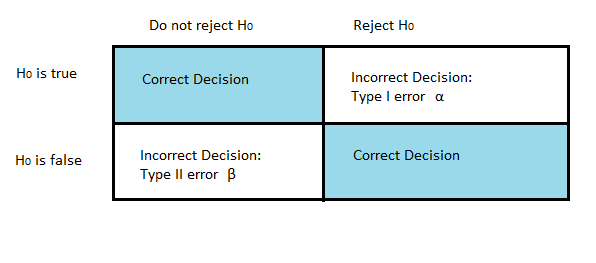
Beta( β) is the probability that you won’t reject the null hypothesis when it is false. The statistical power is the complement of this probability: 1- Β
How to Calculate Statistical Power
Statistical Power is quite complex to calculate by hand. This article on MoreSteam explains it well.
Software is normally used to calculate the power.
Power Analysis
Power analysis is a method for finding statistical power: the probability of finding an effect, assuming that the effect is actually there. To put it another way, power is the probability of rejecting a null hypothesis when it’s false. Note that power is different from a Type II error, which happens when you fail to reject a false null hypothesis. So you could say that power is your probability of not making a type II error.
A Simple Example of Power Analysis
Let’s say you were conducting a drug trial and that the drug works. You run a series of trials with the effective drug and a placebo. If you had a power of .9, that means 90% of the time you would get a statistically significant result. In 10% of the cases, your results would not be statistically significant. The power in this case tells you the probability of finding a difference between the two means, which is 90%. But 10% of the time, you wouldn’t find a difference.
Reasons to run a Power Analysis
You can run a power analysis for many reasons, including:
- To find the number of trials needed to get an effect of a certain size. This is probably the most common use for power analysis–it tells you how many trials you need to do to avoid incorrectly rejecting the null hypothesis.
- To find the power, given an effect size and the number of trials available. This is often useful when you have a limited budget, for say, 100 trials, and you want to know if that number of trials is enough to detect an effect.
- To validate your research. Conducting power analysis is simply put–good science.
Calculating power is complex and is usually always performed with a computer. You can find a list of links to online power calculators here.
Check out our YouTube channel for hundreds of elementary statistics and Probability videos!
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Salkind, N. (2016). Statistics for People Who (Think They) Hate Statistics: Using Microsoft Excel 4th Edition.