You may want to read this article first: What is a Tangent Line?
Watch the video or read on below:
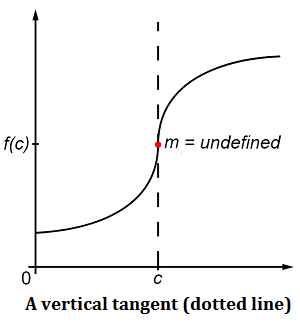 A tangent of a curve is a line that touches the curve at one point. It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient (slope) of the curve is infinite and undefined. On a graph, it runs parallel to the y-axis.
A tangent of a curve is a line that touches the curve at one point. It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient (slope) of the curve is infinite and undefined. On a graph, it runs parallel to the y-axis.
How to Find the Vertical Tangent
General Steps to find the vertical tangent in calculus and the gradient of a curve:
- Find the derivative of the function. The derivative (dy/dx) will give you the gradient (slope) of the curve.
- Find a value of x that makes dy/dx infinite; you’re looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x.
Vertical Tangent in Calculus Example
Example Problem: Find the vertical tangent of the curve y = √(x – 2).
Step 1: Differentiate y = √(x – 2). You can use your graphing calculator, or perform the differentiation by hand (using the power rule and the chain rule). I differentiated the function with this online calculator (which also shows you the steps!):
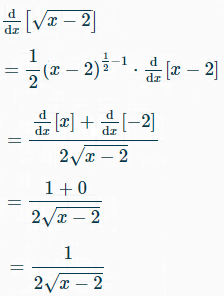
Step 2: Look for values of x that would make dy/dx infinite. This is really where strong algebra skills come in handy, although for this example problem all you need to recognize what happens if you put a “2” into the derivative equation:
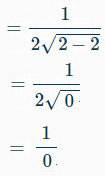
Division by zero is undefined. This means that the gradient of the curve is infinite (i.e., vertical) when x = 2.
The vertical tangent of the curve is x = 2.
That’s it!
Graphing & Tables
If you aren’t able to immediately see where your function might return zero, you’ve got two options:
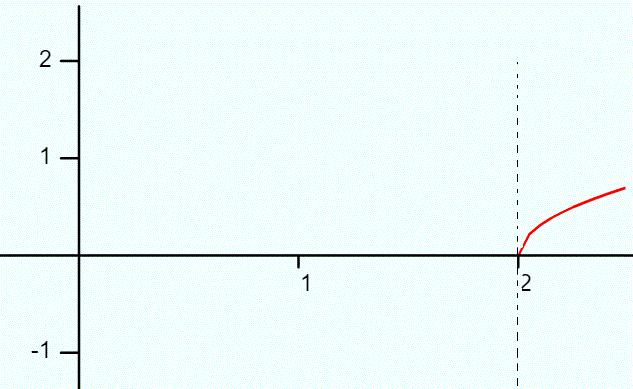
- Graph the function—so you can see where the graph might have a vertical tangent. I used this handy HRW calculator to get the above graph of y = √(x – 2). It’s gairly clear that there’s a vertical tangent at x = 2, though you may want to go through the calculus/algebra anyway to prove it.
- Make a table of values and test for several values of x.
The second option can be very time consuming; Strong algebra skills (like knowing when an equation might result in division by zero) will help you to avoid having to make a table.
Tips:
- Some curves will have more than one vertical tangent. Always make sure you have found all the values of x that make the gradient infinite. You can use graph-plotting software to check by eye for places where the gradient becomes vertical.
- For more tips on where functions might return zero, see the “Guess & Check” section of the Domain and Range article.