Probability > Disjoint Events
What are Disjoint Events?
Disjoint events cannot happen at the same time. In other words, they are mutually exclusive.
Put in formal terms, events A and B are disjoint if their intersection is zero:
P(A∩B) = 0.
You’ll sometimes see this written as:
P(A and B) = 0.
The two terms are equivalent.
Disjoint events are disjointed, or not connected. Another way of looking at disjoint events are that they have no outcomes in common. This definition can be easier to wrap your head around if you think of the opposite: overlapping events have one or more outcomes in common.
Examples of Disjoint Events
- A football game can’t be held at the same time as a rugby game on the same field.
- Heading East and West at the same time is impossible.
- Tossing a coin and getting a heads and a tails at the same time is impossible.
- You can’t take the bus and the car to work at the same time.
- You can’t get a pay raise and a pay decrease at the same time.
- Your dog can’t be both a purebred dog and a mutt.
The following Venn diagram shows two possible events (disjoint and overlapping) for rolling a single die. The diagram on the left shows that the intersection is zero (therefore, these are disjoint). As the diagram on the right does have an intersection, these events are not disjoint. The intersection of the two events is the empty set.
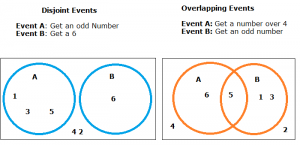
Probability of Disjoint Events
Assuming you’ve figured out that your events are disjoint (using the definition above), you can figure out the probabilities by adding them together:
P(A or B) = P(A) + P(B)
Which can also be rewritten as:
P(A∪B) = P(A) + P(B)
If one or another disjoint event must happen, then the events are complementary events.