Statistics Definitions > Direction of Association
Direction of Association: Overview
Watch the video for an overview:
In Statistics, association tells you whether two variables are related. The direction of the association is always symbolized by a sign either positive (+) or negative (-).
There are two directions of association: positive association and negative association. Positive association is also the same as a positive correlation coefficient and negative association is the same as a negative correlation coefficient. The difference between association and correlation is that correlation is always associated with some kind of correlation coefficient.
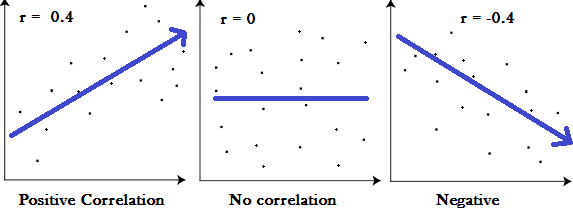
Positive Direction of Association
Two variables have a positive association / correlation when the values of one variable tend to increase as the values of the other variable increase. A perfect positive association means that a relationship appears to exist between two variables, and that relationship is positive 100% of the time. In statistics, a perfect positive association is represented by the value +1.00, while a 0.00 indicates no association. An example of positive association is, the more time you study the higher the chances that you will get a good grade (although it’s not necessarily a perfect correlation!).
Negative Direction of Association
Two variables have negative association when the values of one variable tend to decrease as the values of the other variable increase. In statistics, a perfect negative association is represented by the value -1.00, while a 0.00 indicates no association. A perfect negative association means that the relationship that appears to exist between two variables is negative 100% of the time. It is also possible that two variables may be negatively associated in some, but not all, cases. An example of negative association: the more time you spend chatting with friends means the less time you have for studying.
The direction of association would always depend on the variables that you have whether both variables are moving in one direction or either of the variables are going in opposite directions.