Acyclic Graph & Directed Acyclic Graph: Definition, Examples

Descriptive Statistics > Directed Acyclic Graph

Directed acyclic graphs (DAGs) are used to model probabilities, connectivity, and causality. A “graph” in this sense means a structure made from nodes and edges.

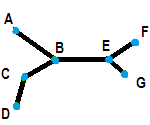
Nodes are usually denoted by circles or ovals (although technically they can be any shape of your choosing).
Edges are the connections between the nodes. An edge connects two nodes. They are usually represented by lines, or lines with arrows.

DAGs are based on basic acyclic graphs.

What is an Acyclic Graph?

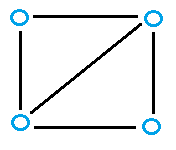
An acyclic graph is a graph without cycles (a cycle is a complete circuit). When following the graph from node to node, you will never visit the same node twice.

minimum spanning tree — This graph (the thick black line) is acyclic, as it has no cycles (complete circuits).

A connected acyclic graph, like the one above, is called a tree. If one or more of the tree “branches” is disconnected, the acyclic graph is a called a forest.

This graph has a complete circuit and so is not acyclic.

What is a Directed Acyclic Graph?

A directed acyclic graph is an acyclic graph that has a direction as well as a lack of cycles.

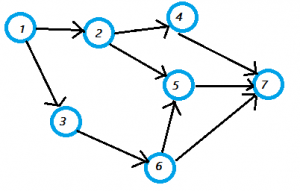
The parts of the above graph are:

Integer = the set for the Vertices.
Vertices set = {1,2,3,4,5,6,7}.
Edge set = {(1,2), (1,3), (2,4), (2,5), (3,6), (4,7), (5,7), (6,7)}.

A directed acyclic graph has a topological ordering. This means that the nodes are ordered so that the starting node has a lower value than the ending node. A DAG has a unique topological ordering if it has a directed path containing all the nodes; in this case the ordering is the same as the order in which the nodes appear in the path.

In computer science, DAGs are also called wait-for-graphs. When a DAG is used to detect a deadlock, it illustrates that a resources has to wait for another process to continue.