Calculators > Interquartile range calculator
This interquartile range calculator finds the IQR for you, along with the 25th percentile, the 50th percentile (the median) and the 75th percentile. The calculator then subtracts the 75th percentile from the 25th percentile to find the interquartile range using the formula Q3 – Q1 = IQR. Just type your numbers into the text box and click the “Find the interquartile range” button! Read below for more instructions.
- 25th Percentile:
- 50th Percentile:
- 75th Percentile:
- Interquartile Range:
Tip: You don’t have to enter your numbers separated by commas in the text box; you can just type in a list of numbers and the calculator will add the commas for you!
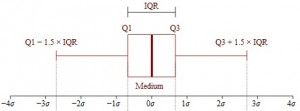
The Interquartile Range Calculator enables you to enter a series of numbers and get the interquartile range without having to solve the interquartile range equation. The interquartile range is the difference between the third quartile and the first quartile in a data set, giving the middle 50%. The interquartile range is a measure of spread; it’s used to build box plots, determine normal distributions and as a way to determine outliers.
Contents:
Click to skip to the section:
How to use the Interquartile Range Calculator
Example 1:
Sample question: Find the interquartile range for this set of numbers: 1, 2, 4, 5, 7, 9, 10, 14, 17:
Step 1: Type your numbers into the text box. The commas are optional; you can just separate each number with a space if you like. If you don’t enter commas, the calculator will put the commas in for you.
Step 2: Press the “Find the Interquartile Range!” button.
Step 3: Scroll down to find the solution. The calculator will give you the interquartile range (which for this particular set of data is 9) and it also returns the 1st quartile (25th percentile), 2nd quartile (50th percentile — the median) and the third quartile (75th percentile).
25th Percentile: 3
50th Percentile: 7
75th Percentile: 12
Interquartile Range: 9
Tip: If you wanted to figure out the interquartile range manually, the formula the calculator uses is IQR = Q3 – Q1 =
9.5 – 3 = 6.5
Example 2
Sample Question: Find the interquartile range for the following data set: 12, 13, 15, 18, 19, 22, 88, 89, 90, 91, 92, 93, 95, 98, 99, 101, 101, 103, 105, 106, 107, 108, 109, 200, 201, 201, 203, 204, 215, 216, 217, 222, 223, 224, 225, 227, 229, 230, 232, 245, 246, 250, 258, 270, 271, 271, 272, 273.
Step 1: Type your data into the Data set: box. Separate each number with commas. It may be faster to copy and paste your data if you have a large data set. For this sample question, the data is already separated by commas, so type “12, 13, 15, 18, 19, 22, 88, 89, 90, 91, 92, 93, 95, 98, 99, 101, 101, 103, 105, 106, 107, 108, 109, 200, 201, 201, 203, 204, 215, 216, 217, 222, 223, 224, 225, 227, 229, 230, 232, 245, 246, 250, 258, 270, 271, 271, 272, 273” into the Data Set: box.
Step 2: Click the “Find the Interquartile Range!” button. The interquartile range is displayed at the bottom of the results list, in bold. For the sample data set, the results are:
Results
- 25th Percentile: 94
- 50th Percentile: 200.5
- 75th Percentile: 228
Interquartile Range: 134
Tip: The interquartile range equation is IQR = Q3 – Q1. Therefore, if you need to show your working out (say, for homework), you can substitute the following from the results list into the equation:
75th percentile 200.5 for Q1
25th percentile 228 for Q2
Giving: IQR = Q3 – Q1 = 200.5 – 94 = 134
Quartile Calculator/Quartile Finder
The interquartile range calculator on this site is also a quartile calculator. It not only finds the interquartile range, it finds the first quartile and the third quartile for any set of numerical data.