In game theory, a branch of math that models competition and conflict, a zero-sum game is where one person wins and the other loses. The net change in wealth for this type of game is zero, hence the name of the game. Gambling is an example of a zero-sum game; The wins of one player equal the losses of the other players.
Two-Person Zero-Sum Games
Two-person zero-sum games play an important role in game development. The idea is that each player has a select number of strategies from which to choose; Each strategy has an associated payoff. While it’s possible to have any number of people in a zero-sum game, they can get very complicated to model [1]. However, we can model a two-person game relatively simply with a 2 x 2 matrix.
Watch the video for an example of a two-person zero-sum game: the Squid Game marbles game.
Two-Person Zero-Sum Game Example: Marbles in Squid Game

We can use a matrix to model the marbles game in Netflix’s Squid Game: Two players, player 001 (the old man) and player 456 (Gi-hun), each have a sack of 10 marbles. They take turns hiding “x” marbles in a closed fist. The other player has to guess whether their opponent has an odd number of marbles, or an even number. If the player guesses right, they win the number of marbles in the hand. If they lose, they have to give their opponent “x” marbles. The following matrix models the possible strategies and payoffs. Each number x represents winnings or losses:
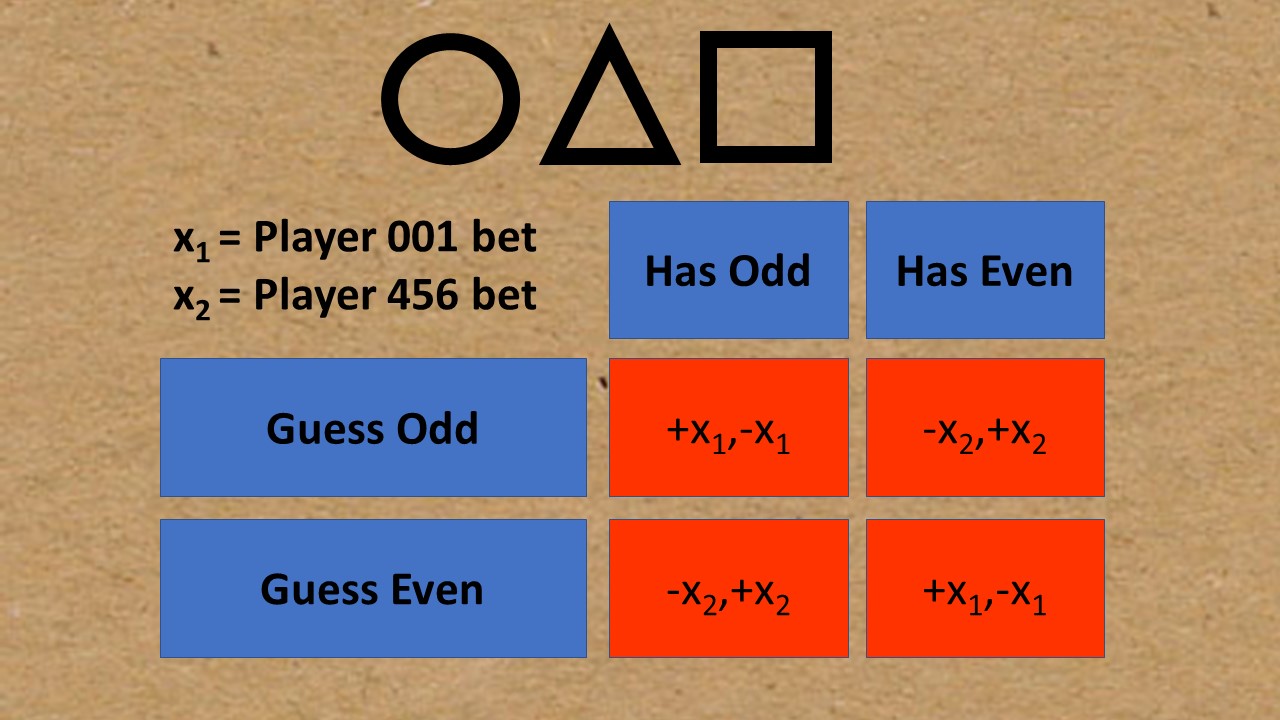
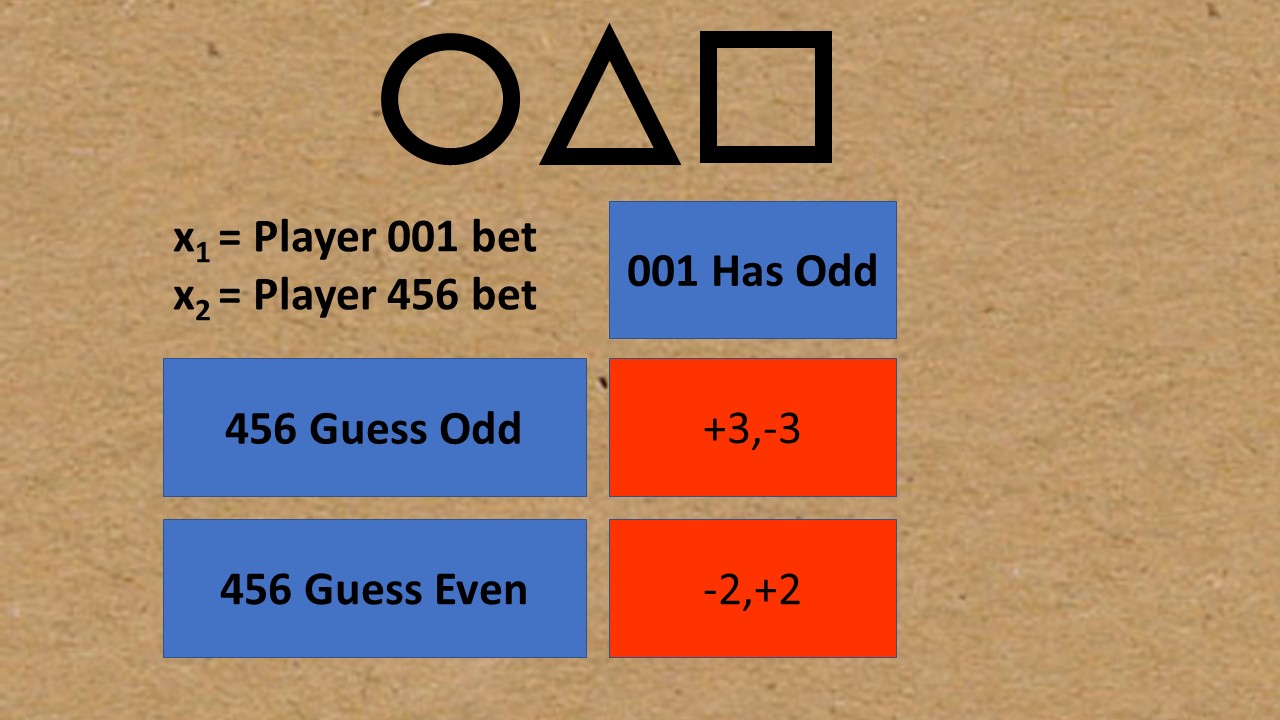
Let’s say it’s player one’s turn to hide marbles, and he chooses to hide 3 (an odd number of marbles). Player 456 bets two marbles. He can either guess odd, or even. If he guesses Odd, he will gain three marbles but player 1 will lose three.
If player 456 guesses even, he will lose his two marbles. But player 1 will gain two marbles. This is shown by the left column of the matrix:
The gains (positive or negative) in the payoff matrix are opposite for each player. Each of the entries in the matrix work the same way, and they all sum to zero (-x + x = 0). Hence, this is a zero-sum game.
The goal of the game is to win all of the marbles; Ordinarily, the matrix can help players choose the best strategy. However, in this particular case, all of the strategies sum to zero, making the odds of winning essentially 50/50 with no best strategy. Any values are possible in the matrix, as long as they represent the value to the player within a certain game; For this particular game, the values are the integers 1 through 19 (if a player has all 20 marbles, he has won the game and so has no need to bet).
Assumptions for the Two Person Zero-Sum Game
One assumption for this model is that the players are greedy, accumulating as much wealth (in this case, marbles) as possible. If you aren’t greedy, fighting for your best interests, you will lose. If you are greedy, and fight for your best interest, you will win the game but hurt your opponents, making this a lose-lose situation rather than a win-win. Another assumption is that the players are rational. In the show, player 001 seems to have dementia, which would mean the assumption of a zero-sum game doesn’t apply. However, we find out that player 001 is faking dementia and is indeed rational (he is, in fact, the game master).
Types of Zero-Sum Games

There are two different types of zero-sum games:
- Perfect information: Players take turns and know the prior moves. These games include one or more optimal strategies. However, as there are multiple possible strategies, they optimal one can be challenging (or even impossible) to calculate. Examples: Chess, Checkers, Connect 4, Tic-Tac-Toe.
- Imperfect information: Play is simultaneous, so players do not know the other player’s move. Some aspect of the game is hidden from players. For example: Bridge, Poker, Rock Paper Scissors.
References
Newberry, P. Game Theory. Retrieved October 5, 2021 from: https://math.colorado.edu/~newberry/Fall11/GameTheory.pdf