What is a Slope? Contents (Click to skip to that section):
More Advanced Topics:
- Slope of a Curve
- Slope of a Tangent Line (Using the Definition of a Limit)
- What is a Slope Field?
- Slope Stability Analysis
1.What is a slope?
The word “slope” in math has roughly the same meaning in math as it has in everyday language:
“…a surface of which one end or side is at a higher level than another; a rising or falling surface.”
It’s slightly more defined when used in math; it’s a number that describes both the direction (positive or negative) and the steepness of the line. It’s usually denoted by the letter m.
2. “Rise over Run”
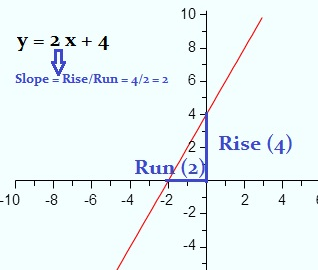
Informally, the slope of a line is found with the catchy phrase “rise over run“. This works with any segment, of any length, for any straight line:
- Find the rise (the length of a segment on the y-axis): The rise (the length of the vertical blue line) in the above picture is 4.
- Find the “run” (the length of a segment on the x-axis): The run (the length of the horizontal blue line) is 2.
- Divide the rise (Step 1) by the run (Step 2): 4/2 = 2.
The slope for this example is 2.
3. Formula for a Straight Line
The formula for a straight lineis:
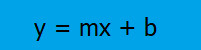
Where:
- b = the y-intercept (where the graph crosses the y-axis),
- m = the slope (i.e. how steep the line is),
- x = a variable.
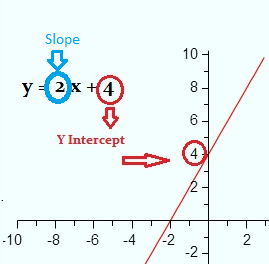
The equation for a straight line (more formally called a “linear equation”) is pretty straightforward to use if you’re given a set of points (example 1). You might also be asked what the slope is for something like y = -9 (example 2) or x = -2.5 (example 3). Although they are both equations (and you might think that y = mx + b will help), you actually need the formula to visualize the answer.*
Examples:
- The slope of the points (2,1) and (4,2) is 1/2 because: (y2 – y1) / (x2 – x1) = (2 – 1) / (4 – 2) = 1/2.
- The slope of y = 9 is zero. The graph of y = 9 is parallel to the x-axis and is flat (i.e. it doesn’t rise or fall at all). You could use the formula to work this out by choosing a couple of random x-values (I’m going to pick 2 and 3):
m = (y2 – y1) / (x2 – x1)
= (9 – 9)/(2 – 1) = 0 / 1 = 0.
As the y-values are constant and will always equal zero when subtracted (i.e. 10 – 10, 4 – 4, -3 – -3), the slope of a line with the equation y = “any number” will always be zero. - The slope of x = 5 is undefined. Any line with an equation of x = “any number” is going to be undefined because look what happens when you plug a couple of points (any random points) into the formula:
m = (2 – 1) / (5 – 5) = 1 / 0 = division by zero is undefined.
*That said, technically you could just memorize that equations with the form y = “any number” has a slope of zero and x = “any number” has an undefined slope.
4. Find the Slope with Algebra
The basic formula for a linear equation is y = mx + b, where “m” is the slope. If you’re given the formula and need to find m, you may need to:
- Look at the formula to find it (example 1),
- Use a little algebra to get the equation in the right form (example 2).
Examples:
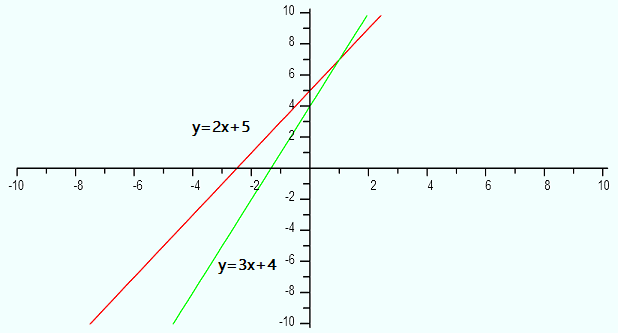
- The slope of y = 2x + 5 is 2.
- The slope of 3y – 9x = 12 is 3, because if we rearrange the formula to look like y = mx + b we get:
Adding 9x to both sides: 3y = 9x + 12.
Dividing by 3 (both sides): y = 3x + 4.
Tip: if there’s nothing before the x (i.e. y = x + 2), the slope is 1, because 1*x = x.
2. Basic Slope Formula: m = rise/run = (y2 – y1) / (x2 – x1).
5. What is a Slope? The Slope of a Curve
The main difference between the slope of a straight line and the slope of a curve is that the slope of a straight line remains constant while the slope of a curve changes between points.
How can we determine what the slope of a curve is if the values are constantly changing? We can do that by using a tangent line. A tangent line is a straight line that touches the plotted curve at a single point. That point is known as the point of tangency.

The tangent line is the small red line at the top of the illustration. Notice how it touches the curved line at a single point.
Formula for Slope of a Curve
The slope of a linear equation can be found with the formula: y = mx + b. When dealing with a curved line, where the slope is changing, you can’t use the same formula. You have to divide the change in y-values by the change in x-values, represented as:
m = change in y/change in x
In order to use this formula to find the slope of a curve, select two points to plug into the formula. Let’s look at an example.
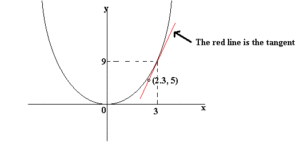
Example question: Find m at the point (9, 3).
In the graph above the tangent line is again drawn in red. The tangent touches the curve at (2.3, 5). Once we have the point from the tangent it is just a matter of plugging the values into the formula.
m = (9-5)/(3-2.3) = 4/.7 = 5.71.
Thus the slope of the curve at point (9, 3) is 5.71.
6. How to Find the Slope of a Tangent Line using the Definition of a Limit
There are several ways to find the slope of a tangent line. The usual way is to take the derivative—It’s equal to the slope of the tangent line at any point. However, if you’re asked to use the ‘definition of a limit’, chances are you haven’t yet covered how to take a derivative yet in your class. The formal definition of the limit can be used to find the slope of the tangent line:
If the point P(x0,y0) is on the curve f, then the tangent line at the point P has a slope given by the formula:
Mtan = lim h→0 f(x0 + h) – f(x0)/h.
Example question: Find the slope of the tangent line to the curve f(x) = 2x2 + 3x – 4 passing through the point P(-1, 5).
Step 1: Replace the “x” in your original function by x + h in the first part of the definition of the limit:
mtan = lim h→0 [2 ( x + h ) 2 ] + 3(x + h) + 4]
Step 2: Subtract your original function and divide by h (all you are doing here is completing the definition for the limit):
mtan = lim h→0 [2 ( x + h ) 2 + 3(x + h) – 4] – [2x2 + 3x – 4 ] / h
Step 3: Solve using algebra. The entire purpose of the following steps is to remove the “h” from the denominator to prevent division by zero:
- FOIL the first part, (x+h)2:
mtan = lim h→0 [2(x2 + 2hx + h2] + 3(x + h) – 4] – [2x2 + 3x – 4 ] / h - Multiply out 3(x + h):
mtan = lim h→0 [2(x2 + 2hx + h2] + 3x + 3h – 4] – [2x2 + 3x – 4 ] / h - Distribute the negative sign
mtan = lim →0 [2(x2 + 2hx + h2] + 3x + 3h – 4] – 2x2 – 3x + 4 / h - Distribute the leading 2:
mtan = lim h→0 [2x2 + 4hx + 2h2 + 3x + 3h – 4 – 2x2 – 3x + 4] / h - Cancel out terms (-3x, -2x2, -4)
mtan = lim h→0 [4hx + 3h 2 + 3h ] / h - Factor the “h” out:
mtan = lim h→0 h (4x + 2h + 3) / h
= lim h→0 4x + 2h + 3 - Set the “2h” to zero (because you are taking the limit, “h” is insignificant). In other words, delete it:
= lim h→0 4x + 3
This gives you the function for the slope of the tangent line.
Step 4: Insert your point into the function:
mtan = 4 (-1) + 3 = -1
The slope of the tangent line is -1.
That’s it!
Back to Top
What is a Slope Field?
A slope field (sometimes called a directional field) represents the solutions to a first order differential equation of a scalar function. A series of tic marks indicate slope. The terms slope field and vector field are sometimes used to mean the same thing, but there is an important difference: All the tic marks in a slope field have the same length; The marks in vector fields vary in length according to the magnitude of the vector.
Essentially, the slope field contains a series of short, bidirectional lines, each one unit long, and each showing the tangent line of the function’s curve at their center points.
Slope fields are also sometimes called direction fields, especially if the vectors retain directional arrows.
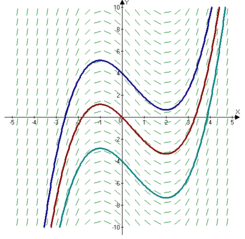
The image below shows the slope field of dy/dx = x2 – x – 2. Three functions are represented by different colors:
- Blue: y = (x3/3)-(x2/2) – 2x + 4,
- Red: y = (x3/3)-(x2/2) – 2x,
- Turquoise: y = (x3/3)-(x2/2) -2x – 4.
Slope Field Applications
Slope fields of even very complex derivatives can be generated quickly and effortlessly by a computer, so they are often used as the first step in understanding a problem before a decision is made on procedures to find an exact solution. They give a good visual understanding of the problem and allow you to see the long term behavior of the solution.
They can also be used as a guide to outline possible solutions. In cases where we don’t have the actual derivative in hand, they can be used by computers to generate numeric solutions through routines like Euler’s method or the Runge–Kutta methods.
Slope Stability Analysis
Slope stability analysis is the study of stability factors, and therefore safety, of both natural and man-made slopes.
Slope stability is generally defined as the resistance of a gradient to “failure”, where failure is collapse or sliding. Analysis typically involves working with two types of equations: equilibrium equations, which apply physics to the field conditions, and constitutive laws (i.e. laws specific to a particular substance) that describe the behavior of the soil.
Types of Analysis
Slope stability analysis is carried on in a number of different ways, but probably the most commonly used method is what is called limit equilibrium analysis. In this analysis one studies the equilibrium between the gradient and a slip surface (this may be a straight line, logarithmic spiral, or the arc of a circle). Shear stresses (τ) are calculated, the available resistance (τf) is calculated, and a ‘factor of safety’ is derived, F= τf / τ.
Some methods of analysis work with the slope as a rigid body, but most divide it into slices and calculate the equilibrium of each individual slice. This has the advantage of allowing an analyst to cater to non-homogeneous surfaces.
Applications
Slope stability analysis plays in an important role in the design and engineering of any architectural structure that contains sloped surfaces, including highway embankments and mountain roads. It also is crucial in earthquake damage prevention, and allows foresters and landscape designers to locate danger areas that are likely to be prone to mud slippages and avalanches.
References
Catanzarita, Filippo. Stability Analysis
Retrieved from https://www.geostru.eu/slope-stability-analysis/ on April 3, 2018
US Army Corps of Engineers. Engineering Manual.
Retrieved from http://www.civil.utah.edu/~bartlett/CVEEN5305/Handout%2010%20-%20EM_1110-2-1902.pdf on April 3, 2018
What is a Slope? References
Barker, Christopher A. A Theoretical Introduction to Slope Fields. Mathematics & Science Learning Center Computer Laboratory. San Joaquin Delta College. Retrieved from http://calculuslab.deltacollege.edu/ODE/7-1/7-1-0-h.html on April 6, 2019.
Kahn, D. Cracking the AP Calculus AB & BC Exams.
Larson & Edwards. Calculus.
Schwartz, Ken. Differential Equations: Slope Field Generator. GeoGebra Retrieved from https://www.geogebra.org/m/MJbBarpr on April 6, 2019.