Shear mapping is a special kind of linear mapping. Points on one axis remain unchanged, while all other points are shifted parallel to that axis.
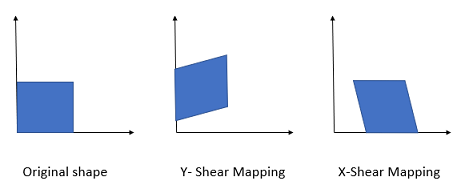
- Each point moves a distance which is proportional to their (signed) perpendicular distance from the axis,
- All points on one side of the stationary axis are transformed in the same direction,
- Areas are always transformed into equal areas.
Example of a Shear Mapping
One example of a shear mapping is the mapping which sends all points (x, y) to (x + 3y, y). In this case the x axis will remain unchanged. Every point is transformed by a distance that is proportional to the signed distance from the x axis. Points on either side of the x axis will be transformed in opposite directions.
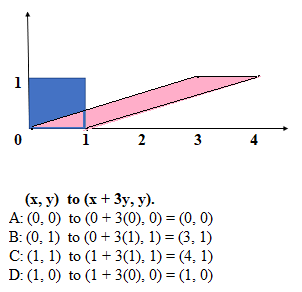
Since every point is moved horizontally, we call this mapping a horizontal shear.
Horizontal and Vertical Shear Mapping
In general, a shear mapping will transform a point (x, y) to (x + ay, y + bx). But the easiest mappings to understand are those for which one of the Cartesian axes is stationary: Horizontal and Vertical Shears.
Horizontal shears, like the transformation in our example above, transform a point with coordinates (x, y) to the point (x + my, y). A vertical shear, similarly, transforms every point (x, y) to the point (x, y + mx).
In these equations m represents a fixed parameter specific to the mapping; we call it the shear factor.
For a horizontal shear, vertical lines that are not identical to the x axis become oblique lines with slope 1/m. The image below shows a horizontal shear in the plane; the shear factor is 1.25. The original grid is in green, and the black dot represents the origin. The green shadow represents the result of the mapping.

References
Research Computing Application Specific Documentation. Using Perspective Mapping. Retrieved from https://rcweb.dartmouth.edu/doc/ibmcxx/en_US/doc/ioc/tasks/t2g2tpmt.htm on November 6, 2019.
Foley & Van Dam, 2D Geometrical Transformations. Retrieved from https://www.cs.brandeis.edu/~cs155/Lecture_06.pdf on November 6, 2019.