Probability of Two Events Occurring Together: Overview
Answering probability questions can seem tricky, but they all really boil down to two things:
- Figuring out if you multiply or add probabilities.
- Figuring out if you have dependent events (one event has an influence on the other) or independent (they have no effect on each other)
Watch the video for an overview and examples:
Should I multiply or add probabilities?
You would add probabilities if you want to find out if one event or another could happen. For example, if you roll a die, and you wanted to know the probability of rolling a 1 or a 6, then you would add the probabilities:
- Probability of rolling a 1: 1/6
- Probability of rolling a 6: 1/6
So the probability of rolling a 1 or a 6 is 1/6 + 1/6 = 2/6 = 1/3.
The probability of both events happening together on the same die is zero, at least with a single throw. But if you wanted to know the probability of rolling a 1 and then rolling a 6, that’s when you would multiply (the probability would be 1/6 * 1/6 = 1/36).
Learning when to add or multiply can get really confusing! The best way to learn when to add and when to multiply is to work out as many probability problems as you can. But, in general:
- If you have “or” in the wording, add the probabilities.
- If you have “and” in the wording, multiply the probabilities.
This is just a general rule: there will be exceptions!
Dependent vs. Independent
Dependent events are connected to each other. For example:
- In order to win at Monopoly, you have to play the game
- In order to find a parking space, you have to drive
- Choosing two cards from a standard deck without replacement (the first choice has a 1/52 chance, the second a 1/51).
Independent events aren’t connected; the probability of one happening has no effect on the other. For example:
- Playing Monopoly isn’t connected to winning at Scrabble.
- Winning the lottery isn’t connected to you winning at Monopoly.
- Choosing a card and then rolling a die are not connected.
If you aren’t sure about the difference between independent and dependent events, you may want to read this article first:
Dependent or Independent event? how to Tell.
Tip: Look for key phrases in the question that tell you if an event is dependent or not. For example, when you are trying to figure out the probability of two events occurring together and the phrase “Out of this group” or “Of this group—” is included, that tells you the events are probably dependent.
Probability of Two Events Occurring Together: Independent
Use the specific multiplication rule formula. Just multiply the probability of the first event by the second. For example, if the probability of event A is 2/9 and the probability of event B is 3/9 then the probability of both events happening at the same time is (2/9)*(3/9) = 6/81 = 2/27.
Example problem: The probability of getting a job you applied for is 45% and the probability of you getting the apartment you applied for is 75%. What is the probability of getting both the new job and the new car?
Step 1: Convert your percentages of the two events to decimals. In the above example:
- 45% = .45.
- 75% = .75.
Step 2: Multiply the decimals from step 1 together:
.45 x .75 = .3375 or 33.75 percent.
The probability of you getting the job and the car is 33.75%
That’s it!
Probability of Two Events Occurring Together: Dependent
The equation you use is slightly different.
P(A and B) = P(A) · P(B|A)
where P(B|A) just means “the probability of B, given that A has already happened”.
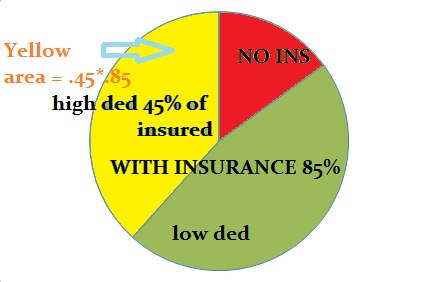
Example problem: Eighty five percent of employees have health insurance. Out of those 85%, 45% had deductibles higher than $1,000. What percentage of people had deductibles higher than $1,000?”
Step 1: Convert your percentages of the two events to decimals. In the above example:
- 85% = .85.
- 45% = .45.
Step 2: Multiply the decimals from step 1 together:
.85 x .45 = .3825 or 38.35 percent.
The probability of someone having a deductible of over $1,000 is 38.35%
That’s how to find the probability of two events occurring together!
Tip: Sometimes it can help to make a sketch or drawing of the problem to visualize what you are trying to do. The following diagram shows the group of people (85% of the population) and the subgroup (45% of the population), making it more obvious that you should be multiplying (because when you translate 45% of the 85% (have insurance with high deductibles) to math, you get .45 * .85).
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company
