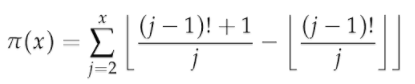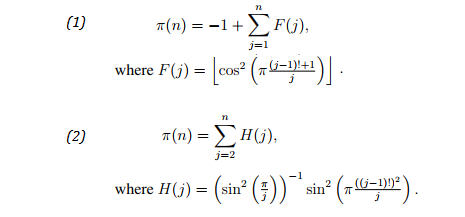Prime Notation: Contents
Click to skip to the section:
What is Prime Notation?
In calculus, prime notation (also called Lagrange notation) is a type of notation for derivatives. The “prime” is a single tick mark (a “prime”) placed after the function symbol, f.
For example: The function f′(x) is read “f-prime of x.”
Higher order derivatives are represented by adding more primes. For example, the third derivative of y with respect to x would be written as y′′′(x). You could, technically, keep adding primes, but most people switch to numerals. For example, the fourth derivative could be written as:
y′′′′(x) = f(4)(x) = f(iv)(x).
Lagrange (1736-1813) first introduced prime notation, but Lagrange prime notation isn’t the only way to symbolize a derivative. Another popular notation is Leibniz notation, which uses the capital Greek letter delta (Δ). Other notations that aren’t used as often include Newton’s Notation and Euler’s notation.
Prime vs Apostophe
Prime notation because it uses the prime symbol (′), which are used to designate units and for other purposes. The prime symbol is commonly used, for example, to designate feet. Don’t confuse it with an apostrophe (′), as they are different characters. Some fonts make it very hard to discern though, and in for most intents and purposes, you can probably get away with just using an apostrophe (except when you’re publishing a paper or book).
Other Meanings for Prime Notation
The prime symbol(′) isn’t exclusively used in differential calculus. Another common use is in geometry, where it is used to denote two distinct, yet similar objects (e.g., vertices B and B’).
The term “Prime Notation” is also sometimes used to mean grouping identical prime numbers together to represent a number. For example, you could write the number 100 as 22 x 55. This is a completely different meaning from the prime notation discussed here.
Connection Between Prime Notation and Numbers
Prime notation and prime numbers are sometimes confused with each other. It’s unfortunate that they are named the same, because there is only a thread of a connection: Some authors occasionally use prime notation (N′)to refer to prime numbers, and that’s where the mathematical connection ends. However, they do share a common meaning for the word “prime”: first.
Prime notation is used to indicate the number of derivatives. A single tick mark (′) denotes the first derivative. This naming convention is attributed to Lagrange, who wrote (in French) “Nous nommerons de plus la premiere fonction derivee f′x, fonction prime; la seconde derivee &prime:′x, fonction seconde;” (Cajori, 1923).
On the other hand, the name prime numbers came from Euclid, who defined prime numbers in The Elements (book 7, definition 1) as follows “A prime number is that which is [divisible] by an unit alone” (Prime Pages, 2021). He used the Greek word “Prôtos”, meaning “first in order of existence”; All numbers can be derived (through multiplication) from primes, which is why they are “First.”
Prime Number Theorem
The Prime Number Theorem helps to calculate probabilities of prime numbers in larger sets. It gives an approximate number of primes less than or equal to any positive real number x.
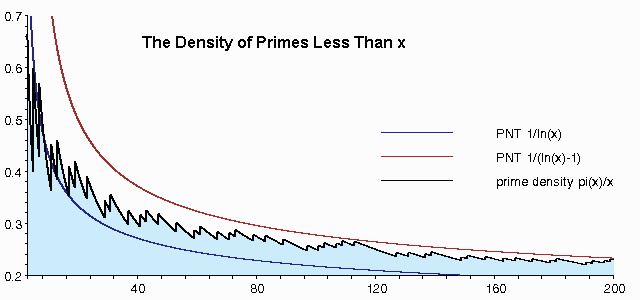
The theorem states that the “density” of prime numbers in the interval from 1 to x is approximately 1 / ln[x].
The following image shows how the approximation works. The black line is the actual density of primes from 0 to 200. For example, if you look at 40 on the chart, the density is 0.3. This is because there are 12 primes up to x = 40: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 and 37. So the actual density is 12/40 = 0.3. The approximation 1/ln(40) = 0.27, which is a reasonable approximation, albeit a little low. The red line in the graph shows an alternate approximation 1/(ln(40)-1) = .37 — which is a little on the high side.
Consequence of the Prime Number Theorem
An interesting consequence of the prime number theorem is that the average distance between consecutive primes (in the vicinity of n) is the logarithm of n (Robbins, 2006). For example, let’s say you took the interval 900 to 1100 (centered at 1,000). There are 30 prime numbers in the interval 900 to 1100.
The total distances are given in parentheses between each pair:
907 (4) 911 (8) 919 (10) 929 (8) 937 (4) 941 (6) 947 (6) 953 (14) 967 (4) 971 (6) 977 (6) 983 (8) 991 (6) 997 (12) 1009 (4) 1013 (6) 1019 (2) 1021 (10) 1031 (2) 1033 (6) 1039 (10) 1049 (2) 1051 (10) 1061 (2) 1063 (6) 1069 (18) 1087 (4) 1091 (2) 1093 (4) 1097
The average distance is 6.55:
(4 + 8 + 10 + 8 + 4 + 6 + 6 + 14 + 4 + 6 + 6 + 8 + 6 + 12 + 4 + 6 + 2 + 10 + 2 + 6 + 10 + 2 + 10 + 2 + 6 + 18 + 4 + 2 + 4) / 29 = 6.55.
Log(1000) gives us about 6.9. That’s a reasonable approximation, which gets a little better for a greater interval; The average distance from 800 to 1200 is 6.8.
Ramanujan prime
A Ramanujan prime is another theory about the number of primes between certain points. The nth Ramanujan prime p is the smallest prime such that there are at least n primes between x and 2x. This is true for any x such that 2x > p.
Prime Counting Function
The prime counting function answers the question “How many primes are there less than or equal to a real number x?” For example, π(2) = 2, because there are two primes less than or equal to 2.
The function is denoted by π(x), which has nothing to do with the number π, ≈3.14. That notation originated with mathematician Edmund Landau in 1909 and is what Eric Weisstein calls “unfortunate”.
The first few values of π(n) for n = {1,2,3,…n} are 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6. For example, at n = 12 there are 5 primes (2, 3, 5, 7, 11).
There’s More Than One Prime Counting Function
There isn’t one single function that can be called the counting function. In fact, there isn’t a simple arithmetic formula for determining π(n). All are relatively complex, and all are approximations (i.e. every one of them has a margins of error).
Two functions from the literature:
- Minác’s formula (Ribenboim, 1995, p181):

- Willans’ formulae (Ribenboim, 1995, p180):

There are many, many more. Kotnik (2008) discusses many of them , along with the history of the prime counting function, in his paper The prime-counting function and its analytic approximations (PDF).
What is a Prime Number?
Prime numbers are whole numbers (numbers that aren’t fractions) greater than 1 that are divisible only by itself and one. For example, 13 is a prime number because it cannot be divided by anything but 13 and 1.
What are primes used for in probability and statistics?
Prime numbers aren’t generally used in statistics (other than those number appearing in data), but statistics and probabilities are used to work with prime numbers in number theory. For example, you might want to find the probability of choosing a prime number from a series of numbers. The odds depend on what interval you choose:
- The probability of finding a prime in the set {0,1,2} is .333, because one out of the three numbers is a prime (1/3 = .333).
- The probability for the set of numbers from 1 to 100 is .25, because 25/100 numbers in that set are primes (which are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97).
Prime numbers look random, but there’s some research using statistical mechanics that suggests a chaos pattern (statistical mechanics is a branch of mathematical physics that studies the behavior of systems). “It is evident that the primes are randomly distributed but, unfortunately, we don’t know what ‘random’ means” (Vaughan, 1990).
Why do we even care about prime numbers in real life or the probability of finding them? You may not realize it, but prime numbers play an important role in many areas of science, including the math behind internet shopping. Prime numbers are the nuts and bolts behind the cryptography that keeps your personal information secure when you shop online.
Is 2 a prime number?
Yes. It’s the first (and only) even prime number.
How many prime numbers are there?
There are an infinite amount of prime numbers. Although new prime numbers are being discovered every day, there’s no end to the amount of primes to be discovered. The proof of this fact goes back to 300 B.C.E. when Euclid outlined it in book IX of The Elements. Proposition 20 states every list of primes (no matter how large) is missing at least one prime number.
What is the Largest Prime Number?
As of the beginning of 2016, the largest prime number was 274,207,281-1 (record stands as of time of writing—September 17, 2017). It is calculated by multiplying 2 by itself 74,207,281 times, then subtracting one. New primes are being found all the time. For the most up-to-date list of the largest prime number, see: GIMPS.
Back to top
References
Borwein, J. and Bailey, D. “Prime Numbers and the Zeta Function.” Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 63-72, 2003.
Cajori, F. (1923). The History of Notations of the Calculus. Annals of Mathematics , Sep., 1923, Second Series, Vol. 25, No. 1 (Sep., 1923), pp.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Feldman, P. Prime Numbers and their statistical properties. Retrieved September 16, 2017 from: http://phillipmfeldman.org/primes/primes.html
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Great Internet Mersenne Prime Search (GIMPS). Retrieved September 17, 2017 from: http://www.mersenne.org/.
Kotnik, T. (2008). The prime-counting function and its analytic
approximations. Adv Comput Math (2008) 29:55–70
DOI 10.1007/s10444-007-9039-2
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Prime Pages. FAQ: Why are Prime Numbers called Primes? Retrieved April 8, 2021 from: https://primes.utm.edu/notes/faq/WhyCalledPrimes.html
Ribenboim, P. (1995). The Little Book of Big Primes. Springer Verlag.
Robbins, N. (2006). Beginning Number Theory. Jones and Bartlett Learning.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 74-76, 1991.
Vaughan, R. (1990). Harald Cramér and the distribution of prime numbers. Retrieved September 16, 2017 from: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.129.6847
Weisstein, Eric W. “Prime Counting Function.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/PrimeCountingFunction.html
Image: Self [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]