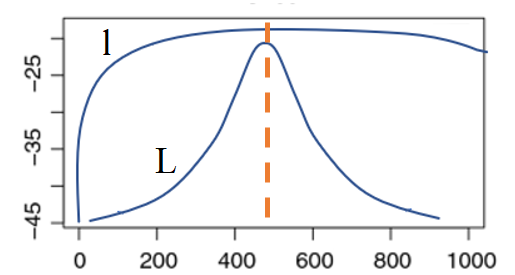
Log Likelihood Function

A likelihood method is a measure of how well a particular model fits the data; They explain how well a parameter (θ) explains the observed data. The logarithms of likelihood, the log likelihood function, does the same job and is usually preferred for a few reasons:

The log likelihood function in maximum likelihood estimations is usually computationally simpler [1].
Likelihoods are often tiny numbers (or large products) which makes them difficult to graph. Taking the natural (base e) logarithm results in a better graph with large sums instead of products.
The log likelihood function is usually (not always!) easier to optimize.

For example, let’s say you had a set of iid observations x₁, x₂…x_n with individual probability density function f_X(x). Their joint density function is:

f_X₁, _X₂…_{X_n}(x₁, x₂…x_n) = f_X(x₁) * f_X(x₂) * … * f_X(x_n) =

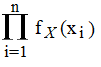
Where:

Π = product (multiplication).

The log of a product is the sum of the logs of the multiplied terms, so we can rewrite the above equation with summation instead of products:

ln[f_X(x₁) * f_X(x₂) * … * f_X(x_n)] =

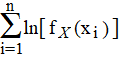
The above relationship leads directly to the log likelihood function[2]:

l(Θ) = ln[L(Θ)].

Although log-likelihood functions are mathematically easier than their multiplicative counterparts, they can be challenging to calculate by hand. They are usually calculated with software.

Formulation of Log-Likelihood Function

The value of the parameter that maximizes the probability of observing data is called a maximum-likelihood estimate. Let’s say we had a set of data d made up of random variables D. We want to use the data to estimate a parameter θ.

Uses of the Log-Likelihood Function

The log likelihood function frequently pops up in financial risk forecasting and probability and statistics—especially in regression analysis / model fitting. For example:

Akaike’s Information Criterion chooses the best model from a set. The basic AIC formula AIC = -2(log-likelihood) + 2K
Likelihood-ratio test: a hypothesis test to choose the best model between two nested models.

References

[1] Robinson, E. (2016). Introduction to Likelihood Statistics. Retrieved April 16, 2021 from: https://hea-www.harvard.edu/AstroStat/aas227_2016/lecture1_Robinson.pdf
[2] Edge, M. (2021). Statistical Thinking from Scratch: A Primer for Scientists.