Frustum: Simple Definition, Volume

Calculus Definitions >

A frustum is a geometrical solid that is made when one plane or two parallel planes cut through a 3-dimensional solid. Typically, that solid is a cone or a pyramid.

Conical Frustum: Frustum of Cone Formula

A conical frustum is what you get when you cut the top off a cone, holding your knife parallel to the base.


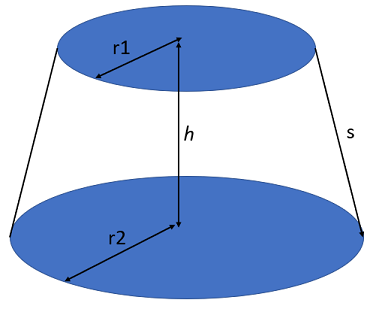
If your truncated cone is based off a right circular cone, it is relatively easy to calculate volume and surface area.

Suppose:

• R₁ is the radius of the base,
• R₂ is the radius of the (new) top.
• h is the height of your truncated solid.

Then the lateral surface area (the entire surface area minus the top and bottom circles) of the solid can be calculated by:

The volume of the frustum is given by:

You can derive this formula from the formulas for the surface area and volume of a cone: Simply subtract the volume (or lateral surface area) of the truncated tip from the volume (or lateral surface area) of the whole. You can also use calculus to derive the formula, as you can see below.

Using Calculus to Derive a Formula for the Volume

Imagine dividing your frustum up into infinitely small slices (dz) over the height z. Then we can write the volume as the integral:


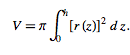
The formula for the radius, r(z), can be written as:


Substitute that in, to get


Since all our R are just constants, that comes out to just


Which happens to be the same as the formula above.

Pyramidal Frustum

The volume formula for square pyramids are nothing new; in fact, they were discussed in ancient Egyptian papyrus around 1850 BC and the formula was given as

Here:

• h is the height of the truncated shape,
• a and b are the top and base side lengths.

The Egyptians, of course, used different variables.

The lateral surface area of the pyramidal frustum is just

h(a + b)/2

As was the case with conical solids, these formulas can be derived from the standard formulas for the volume or surface area of a pyramid through calculus. Alternatively, subtract the volume (or surface area) of the tip from that of the original pyramid.

References

Rohde, U. et. al. (2012). Introduction to Integral Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley & Sons.