Contents:
See also: The Power Rule
Watch the video for a couple of examples of how to eliminate exponents with logarithms:
1. Exponents: Definition
An exponent is a simplified way of saying how many times to multiply a number by itself. When dealing with exponents we need to know which number represents the base number and which is the exponent.
- The base number is the number that is multiplied by itself. It’s usually written in a larger font.
- The exponent tells us how many times to multiply the base number by itself. It’s usually written in a smaller font (as a superscript).
Both are represented in the following example:
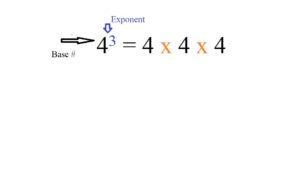
As shown above, 4 is the base number. The exponent is 3. What this tells you is that you’ll be multiplying 4 by itself three times [4 x 4 x 4]. First multiply 4 x 4 to get 16. Then multiply this number by 4 [16 x 4 = 64]. Therefore, 43 equals 64.
You can make two important observations from this example. First, notice how much simpler it is to use an exponent rather than writing out the multiplication in long-form. You could imagine when dealing with much larger exponents how complicated it would be to write it out. Second, as the exponent increases the base number will increase exponentially. There is no limit to how many times a number can be multiplied by itself.
Where the Exponent is 1 or 0
When you see the exponent is 1 then the answer will be the number itself (another way of thinking about this is that any number multiplied by 1 stays the same).
When you see the exponent is 0 then the answer will be 1 no matter what the value of the base number is.
Negative Exponents
A negative exponent tells you to divide the number 1 by the base number. An easy way to remember this is that a negative is the opposite of a positive and division is the opposite of multiplication. Let’s take a look at an example:
8-4
Written out 8 to the negative 4th power is: 1/8/8/8/8
- Divide 1 by 8 which equals 0.125
- Next, divide 0.125 by 8 which equals 0.015625
- Divide 0.015625 by 8 which equals 0.001953125
- Finally, divide 0.001953125 by 8, to get 0.0002441406
2. How to Eliminate Exponents
Exponents can be a tricky factor in dealing with equations, and when exponents have variables in them it becomes even more complicated. It’s possible to eliminate some exponents using the The Power Rule, but this won’t work for exponents over 2. Another way to eliminate exponents is to convert exponents into a more manageable form, with the logarithm function.
If you aren’t familiar with logarithms, then you may want to read the logarithms definition before reading on. Basically, logarithms are simply an exponent in a different form, so that’s why you can use them to eliminate exponents. For example, log10100 = 2 is the same as 102 = 100. More generally, that’s:
The log might also appear in the form ln(x), which is a log taken to the base of e, the natural number.
How to Eliminate Exponents in Calculus: Example
Example Problem: Solve for the value of x if 10 to the 5x power plus 10 is equal to 20.
Step 1: Set up the equation from the information given in the question.
105x + 10 = 20
Step 2: Take 10 from both sides to eliminate the 10 near the variable. This is a basic algebra step, but still an important one.
105x + 10 – 10 = 20 – 10
giving:
105x = 10
Step 3: Take the log of both sides.
log(105x) = log(10)
Step 4: Apply the logarithms rule that states log_b(ac) = c * log_b(a).1
Using this, we can move the variable out of the exponent and leave it in a form we can simplify. If you recall that a log without a subscript is considered a base of 10, you can easily simplify log_10(10) = y as 1, due to by = x being 101 = 10.
5x * 1 = 1
Step 5: Divide both sides by 5 to isolate the variable. This will give you a final answer of 1/5, or .2.
5x/5 = 1/5 -> x = 1/5 = 0.2
Notes
1: If you need a refresher on log rules, see Mathematical prerequisites— scroll down to 5. Exponents and Logarithms.
References
York University Course Archive. Mathematical Prerequisites. Retrieved January 1, 2019 from: https://www.eecs.yorku.ca/course_archive/2011-12/W/3101/prereq.pdf