Types of Graphs > Minimum Spanning Tree
Contents:
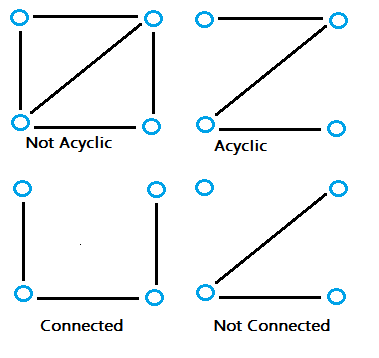
What is a Minimum Spanning Tree?
A minimum spanning tree is a special kind of tree that minimizes the lengths (or “weights”) of the edges of the tree. An example is a cable company wanting to lay line to multiple neighborhoods; by minimizing the amount of cable laid, the cable company will save money.
A tree has one path joins any two vertices. A spanning tree of a graph is a tree that:
- Contains all the original graph’s vertices.
- Reaches out to (spans) all vertices.
- Is acyclic. In other words, the graph doesn’t have any nodes which loop back to itself.
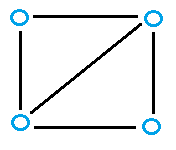
Even the simplest of graphs can contain many spanning trees. For example, the following graph:
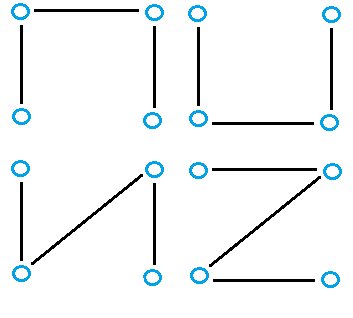
…has many possibilities for spanning trees, including:
Finding Minimum Spanning Trees
As you can probably imagine, larger graphs have more nodes and many more possibilities for subgraphs. The number of subgraphs can quickly reach into the millions, or billions, making it very difficult (and sometimes impossible) to find the minimum spanning tree. Additionally, the lengths usually have different weights; one 5m long edge might be given a weight of 5, another of the same length might be given a weight of 7.
A few popular algorithms for finding this minimum distance include: Kruskal’s algorithm, Prim’s algorithm and Boruvka’s algorithm. These work for simple spanning trees. For more complex graphs, you’ll probably need to use software.
Kruskal’s algorithm example
Find the edge with the least weight and highlight it. For this example graph, I’ve highlighted the top edge (from A to C) in red. It has the lowest weight (of 1):
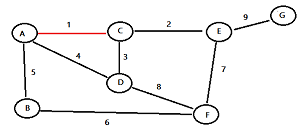
Find the next edge with the lowest weight and highlight it:
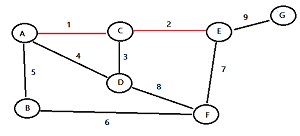
Continue selecting the lowest edges until all nodes are in the same tree.
Notes:
- If you have more than one edge with the same weight, choose an edge with the lowest weight.
- Be careful not to complete a cycle (route one node back to itself). If your choice completes a cycle, discard your choice and move onto the next largest weight.
The finished minimum spanning tree for this example looks like this:
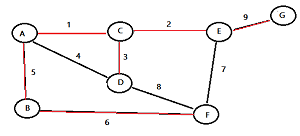
What is Prim’s Algorithm?
Prim’s algorithm is one way to find a minimum spanning tree (MST).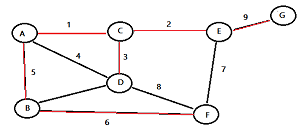
How to Run Prim’s Algorithm
Step 1: Choose a random node and highlight it. For this example, I’m choosing node C.
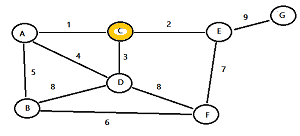
Step 2: Find all of the edges that go to un-highlighted nodes. For this example, node C has three edges with weights 1, 2, and 3. Highlight the edge with the lowest weight. For this example, that’s 1.
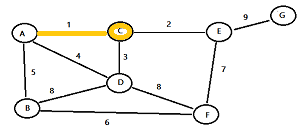
Step 3: Highlight the node you just reached (in this example, that’s node A).
Step 4: Look at all of the nodes highlighted so far (in this example, that’s A And C). Highlight the edge with lowest weight (in this example, that’s the edge with weight 2).
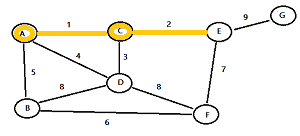
Note: if you have have more than one edge with the same weight, pick a random one.
Step 5: Highlight the node you just reached.
Step 6: Highlight the edge with the lowest weight. Choose from all of the edges that:
- Come from all of the highlighted nodes.
- Reach a node that you haven’t highlighted yet
Step 7: Repeat steps 5 and 6 until you have no more un-highlighted nodes. For this particular example, the specific steps remaining are:
- a. Highlight node E.
- b. Highlight edge 3 and then node D.
- c. Highlight edge 5 and then node B.
- d. Highlight edge 6 and then node F.
- e. Highlight edge 9 and then node G.
- Cluster Analysis.
- Real-time face tracking and verification (i.e. locating human faces in a video stream).
- Protocols in computer science to avoid network cycles.
- Entropy based image registration.
- Max bottleneck paths.
- Dithering (adding white noise to a digital recording in order to reduce distortion).
The finished graph is shown at the bottom right of this image:
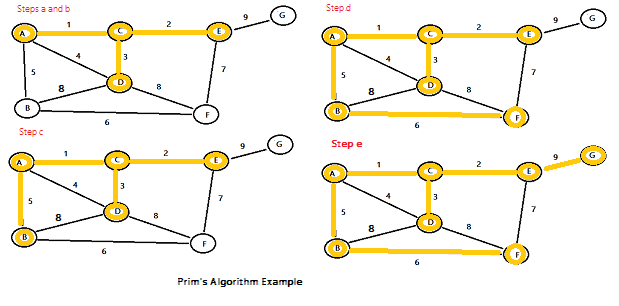
That’s it!
Real Life Applications
Minimum spanning trees are used for network designs (i.e. telephone or cable networks). They are also used to find approximate solutions for complex mathematical problems like the Traveling Salesman Problem. Other, diverse applications include:
References
Wu, B. & Chao, K. (2004). Spanning Trees and Optimization Problems. Chapman and Hall/CRC.