Non normal distribution > The Maxwell-Boltzmann Distribution
What is the Maxwell-Boltzmann distribution?
The Maxwell-Boltzmann distribution is a probability distribution mainly used in physics and statistical mechanics. The distribution, which describes the kinetic energy of air particles in a particular sample, was devised by James C. Maxwell and Ludwig Boltzmann. In simple terms, the kinetic energy of a particle in a system is a particle’s speed. The area under the distribution represents the total number of particles in a sample.
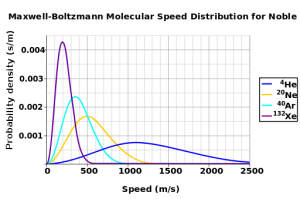 The temperature of a gas is proportional to average kinetic energy in the system. In other words, the average kinetic energy is higher at higher temperatures. The Maxwell-Boltzmann distribution plots number of molecules on the y- axis against speed on the x-axis. It tells you which speeds are more likely in a system. The distribution is dependent on the temperature of the system and the mass of the particle.
The temperature of a gas is proportional to average kinetic energy in the system. In other words, the average kinetic energy is higher at higher temperatures. The Maxwell-Boltzmann distribution plots number of molecules on the y- axis against speed on the x-axis. It tells you which speeds are more likely in a system. The distribution is dependent on the temperature of the system and the mass of the particle.
Activation Energy: Why Bonds Break and Form
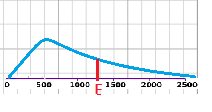 The distribution helps to explain why bonds break and new bonds form. In a given system, a particle must have a certain kinetic energy to collide with another particle and break/form a bond (called the activation energy). The activation energy can be represented by a point on the x-axis of the distribution; the area under the curve to the right of the activation energy point(labeled E on the graph) is the number of particles in the system that have the energy necessary for new bond formation. In general at higher temperatures, more particles have sufficient energy to react.
The distribution helps to explain why bonds break and new bonds form. In a given system, a particle must have a certain kinetic energy to collide with another particle and break/form a bond (called the activation energy). The activation energy can be represented by a point on the x-axis of the distribution; the area under the curve to the right of the activation energy point(labeled E on the graph) is the number of particles in the system that have the energy necessary for new bond formation. In general at higher temperatures, more particles have sufficient energy to react.
Adding a catalyst to the system lowers the activation energy without changing the shape of the distribution. As the activation energy point moves to the left of the graph, the area under the curve becomes greater. In other words, more particles can make and break bonds.