What is Bayes’ Theorem?
Watch the video for a quick example of working a Bayes’ Theorem problem:
Bayes’ theorem is a way to figure out conditional probability. Conditional probability is the probability of an event happening, given that it has some relationship to one or more other events. For example, your probability of getting a parking space is connected to the time of day you park, where you park, and what conventions are going on at any time. Bayes’ theorem is slightly more nuanced. In a nutshell, it gives you the actual probability of an event given information about tests.
- “Events” Are different from “tests.” For example, there is a test for liver disease, but that’s separate from the event of actually having liver disease.
- Tests are flawed: just because you have a positive test does not mean you actually have the disease. Many tests have a high false positive rate. Rare events tend to have higher false positive rates than more common events. We’re not just talking about medical tests here. For example, spam filtering can have high false positive rates. Bayes’ theorem takes the test results and calculates your real probability that the test has identified the event.
The Formula
Bayes’ Theorem (also known as Bayes’ rule) is a deceptively simple formula used to calculate conditional probability. The Theorem was named after English mathematician Thomas Bayes (1701-1761). The formal definition for the rule is:
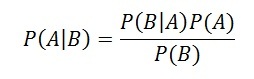
In most cases, you can’t just plug numbers into an equation; You have to figure out what your “tests” and “events” are first. For two events, A and B, Bayes’ theorem allows you to figure out p(A|B) (the probability that event A happened, given that test B was positive) from p(B|A) (the probability that test B happened, given that event A happened). It can be a little tricky to wrap your head around as technically you’re working backwards; you may have to switch your tests and events around, which can get confusing. An example should clarify what I mean by “switch the tests and events around.”
Bayes’ Theorem Example #1
You might be interested in finding out a patient’s probability of having liver disease if they are an alcoholic. “Being an alcoholic” is the test (kind of like a litmus test) for liver disease.
- A could mean the event “Patient has liver disease.” Past data tells you that 10% of patients entering your clinic have liver disease. P(A) = 0.10.
- B could mean the litmus test that “Patient is an alcoholic.” Five percent of the clinic’s patients are alcoholics. P(B) = 0.05.
- You might also know that among those patients diagnosed with liver disease, 7% are alcoholics. This is your B|A: the probability that a patient is alcoholic, given that they have liver disease, is 7%.
Bayes’ theorem tells you:
P(A|B) = (0.07 * 0.1)/0.05 = 0.14
In other words, if the patient is an alcoholic, their chances of having liver disease is 0.14 (14%). This is a large increase from the 10% suggested by past data. But it’s still unlikely that any particular patient has liver disease.
More Bayes’ Theorem Examples
Bayes’ Theorem Problems Example #2
Another way to look at the theorem is to say that one event follows another. Above I said “tests” and “events”, but it’s also legitimate to think of it as the “first event” that leads to the “second event.” There’s no one right way to do this: use the terminology that makes most sense to you.
In a particular pain clinic, 10% of patients are prescribed narcotic pain killers. Overall, five percent of the clinic’s patients are addicted to narcotics (including pain killers and illegal substances). Out of all the people prescribed pain pills, 8% are addicts. If a patient is an addict, what is the probability that they will be prescribed pain pills?
Step 1: Figure out what your event “A” is from the question. That information is in the italicized part of this particular question. The event that happens first (A) is being prescribed pain pills. That’s given as 10%.
Step 2: Figure out what your event “B” is from the question. That information is also in the italicized part of this particular question. Event B is being an addict. That’s given as 5%.
Step 3: Figure out what the probability of event B (Step 2) given event A (Step 1). In other words, find what (B|A) is. We want to know “Given that people are prescribed pain pills, what’s the probability they are an addict?” That is given in the question as 8%, or .8.
Step 4: Insert your answers from Steps 1, 2 and 3 into the formula and solve.
P(A|B) = P(B|A) * P(A) / P(B) = (0.08 * 0.1)/0.05 = 0.16
The probability of an addict being prescribed pain pills is 0.16 (16%).
Example #3: the Medical Test
A slightly more complicated example involves a medical test (in this case, a genetic test):
There are several forms of Bayes’ Theorem out there, and they are all equivalent (they are just written in slightly different ways). In this next equation, “X” is used in place of “B.” In addition, you’ll see some changes in the denominator. The proof of why we can rearrange the equation like this is beyond the scope of this article (otherwise it would be 5,000 words instead of 2,000!). However, if you come across a question involving medical tests, you’ll likely be using this alternative formula to find the answer:
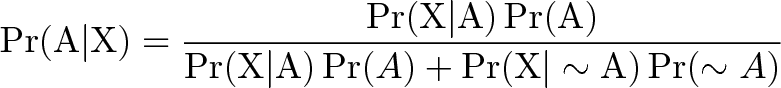
Watch the video for a Bayes’ Theorem example:
1% of people have a certain genetic defect.
90% of tests for the gene detect the defect (true positives).
9.6% of the tests are false positives.
If a person gets a positive test result, what are the odds they actually have the genetic defect?
The first step into solving Bayes’ theorem problems is to assign letters to events:
- A = chance of having the faulty gene. That was given in the question as 1%. That also means the probability of not having the gene (~A) is 99%.
- X = A positive test result.
So:
- P(A|X) = Probability of having the gene given a positive test result.
- P(X|A) = Chance of a positive test result given that the person actually has the gene. That was given in the question as 90%.
- p(X|~A) = Chance of a positive test if the person doesn’t have the gene. That was given in the question as 9.6%
Now we have all of the information we need to put into the equation:
P(A|X) = (.9 * .01) / (.9 * .01 + .096 * .99) = 0.0865 (8.65%).
The probability of having the faulty gene on the test is 8.65%.
Bayes’ Theorem Problems #4: A Test for Cancer
I wrote about how challenging physicians find probability and statistics in my post on reading mammogram results wrong. It’s not surprising that physicians are way off with their interpretation of results, given that some tricky probabilities are at play. Here’s a second example of how Bayes’ Theorem works. I’ve used similar numbers, but the question is worded differently to give you another opportunity to wrap your mind around how you decide which is event A and which is event X.
Q. Given the following statistics, what is the probability that a woman has cancer if she has a positive mammogram result?
- One percent of women over 50 have breast cancer.
- Ninety percent of women who have breast cancer test positive on mammograms.
- Eight percent of women will have false positives.
Step 1: Assign events to A or X. You want to know what a woman’s probability of having cancer is, given a positive mammogram. For this problem, actually having cancer is A and a positive test result is X.
Step 2: List out the parts of the equation (this makes it easier to work the actual equation):
P(A)=0.01
P(~A)=0.99
P(X|A)=0.9
P(X|~A)=0.08
Step 3: Insert the parts into the equation and solve. Note that as this is a medical test, we’re using the form of the equation from example #2:
(0.9 * 0.01) / ((0.9 * 0.01) + (0.08 * 0.99) = 0.10.
The probability of a woman having cancer, given a positive test result, is 10%.
Remember when (up there ^^) I said that there are many equivalent ways to write Bayes Theorem? Here is another equation, that you can use to figure out the above problem. You’ll get exactly the same result:
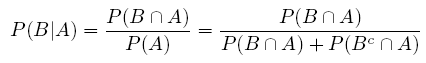
The main difference with this form of the equation is that it uses the probability terms intersection(∩) and complement (c). Think of it as shorthand: it’s the same equation, written in a different way.
In order to find the probabilities on the right side of this equation, use the multiplication rule:
P(B ∩ A) = P(B) * P(A|B)
The two sides of the equation are equivalent, and P(B) * P(A|B) is what we were using when we solved the numerator in the problem above.
P(B) * P(A|B) = 0.01 * 0.9 = 0.009
For the denominator, we have P(Bc ∩ A) as part of the equation. This can be (equivalently) rewritten as P(Bc*P(A|Bc). This gives us:
P(Bc*P(A|Bc) = 0.99 * 0.08 = 0.0792.
Inserting those two solutions into the formula, we get:
0.009 / (0.009 + 0.0792) = 10%.
Bayes’ Theorem Problems: Another Way to Look at It.
Bayes’ theorem problems can be figured out without using the equation (although using the equation is probably simpler). But if you can’t wrap your head around why the equation works (or what it’s doing), here’s the non-equation solution for the same problem in #1 (the genetic test problem) above.
Step 1: Find the probability of a true positive on the test. That equals people who actually have the defect (1%) * true positive results (90%) = .009.
Step 2: Find the probability of a false positive on the test. That equals people who don’t have the defect (99%) * false positive results (9.6%) = .09504.
Step 3: Figure out the probability of getting a positive result on the test. That equals the chance of a true positive (Step 1) plus a false positive (Step 2) = .009 + .09504 = .0.10404.
Step 4: Find the probability of actually having the gene, given a positive result. Divide the chance of having a real, positive result (Step 1) by the chance of getting any kind of positive result (Step 3) = .009/.10404 = 0.0865 (8.65%).
Other forms of Bayes’ Theorem
Bayes’ Theorem has several forms. You probably won’t encounter any of these other forms in an elementary stats class. The different forms can be used for different purposes. For example, one version uses what Rudolf Carnap called the “probability ratio“. The probability ratio rule states that any event (like a patient having liver disease) must be multiplied by this factor PR(H,E)=PE(H)/P(H). That gives the event’s probability conditional on E. The Odds Ratio Rule is very similar to the probability ratio, but the likelihood ratio divides a test’s true positive rate divided by its false positive rate. The formal definition of the Odds Ratio rule is OR(H,E)=PH,(E)/P~H(E).
Bayesian Spam Filtering
Although Bayes’ Theorem is used extensively in the medical sciences, there are other applications. For example, it’s used to filter spam. The event in this case is that the message is spam. The test for spam is that the message contains some flagged words (like “viagra” or “you have won”). Here’s the equation set up (from Wikipedia), read as “The probability a message is spam given that it contains certain flagged words”:
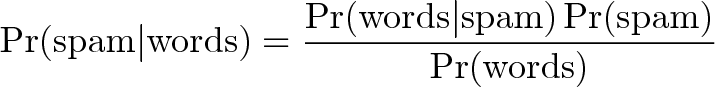
The actual equations used for spam filtering are a little more complex; they contain more flags than just content. For example, the timing of the message, or how often the filter has seen the same content before, are two other spam tests.
Next: Inverse Probability Distribution
References
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.