In probability, the trinomial coefficient (sometimes called the central trinomial coefficient) is the number of ways of partitioning a set of objects into three disjoint subsets.
The value of the trinomial coefficient can be calculated as (Hilton et al., 2002; Kuri-Morales & Simari, 2002):
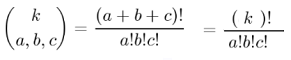
Where:
- ! is a factorial,
- k is the number of objects you want to partition (non-negative integer),
- a, b, c, are the three subsets (also must be non-negative integers),
Trinomial Coefficient and the Trinomial Theorem
Trinomial coefficients appear in the trinomial theorem, which expands a trinomial (x + y + z)k as the algebraic coefficient of xa yb zc:
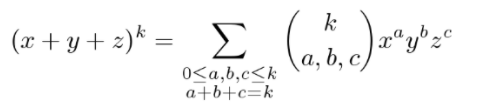
Relation to Binomial Coefficient
The trinomial coefficient is a close relative of the binomial coefficient:
- The trinomial coefficient appears in the expansion of a trinomial (x + y + z)k and is the number of ways of partitioning three sets.
- The binomial coefficient appears in the expansion of a binomial (x + y)k, and is the number of ways of partitioning two sets.
The Trinomial Triangle
The trinomial triangle, an extension of Pascal’s triangle, gives the coefficients of the expansion (1 + x + x2)k.

The entries in each row represent “k”. For example, the second row (k = 2) has entries 1 2 3 2 1, giving the expansion
(1 + x + x2)2 = 1 + 2x + 3x2 + 2x3 + x4.
References
Engelward, A. The Analogies between Binomial and Trinomial Coefficients. Retrieved September 29, 2020 from: http://people.math.harvard.edu/~engelwar/MathS305/Trinomial%20Coefficients.pdf
Graham, D. & Allinson, N. (1998). Characterizing Virtual Eigensignatures for General Purpose Face Recognition. Face Recognition From Theory to Application 163, 446-456.
Hilton, P. et al. (2002). Mathematical Vistas: From a Room with Many Windows. Springer.
Kuri-Morales, A. & Simari, G. (2010). Advances in Artificial Intelligence – IBERAMIA 2010. 12th Ibero-American Conference on AI, Bahía Blanca, Argentina, November 1-5, 2010, Proceedings. Springer Berlin Heidelberg.