You may want to read about factors and blocks first. See:
What is a Split-Plot Design?
When some factors (independent variables) are difficult or impossible to change in your experiment, a completely randomized design isn’t possible. The result is a split-plot design, which has a mixture of hard to randomize (or hard-to-change) and easy-to-randomize (or easy-to-change) factors. The hard-to-change factors are implemented first, followed by the easier-to-change factors.
The “Plot” part of split-plot originally comes from a plot of land in agriculture. Split-plots were invented by Fisher (1935) and it has been suggested that all agricultural experiments are split-plot designs (Box et. al, 2005). Although these designs are commonly seen in industry, they can also be used across a wide variety of disciplines, including medicine. In fact, any experiment where one of your factors is difficult to change or randomize is a candidate for a split-plot design.
Example
You want to study the effects of two irrigation methods (factor 1) and two different fertilizer types (factor 2) on four different fields (“whole plots”). However, you run into a practical problem with randomization. While a field can easily be split into two for the two different fertilizers, the field cannot easily be split into two for irrigation: One irrigation system normally covers a whole field and the systems are expensive to replace.
Step 1: Randomize the fixed or hard-to-change factor (in this example, that’s the irrigation method) among the four fields:
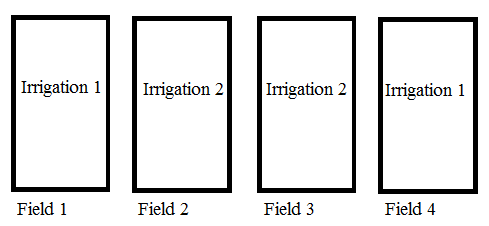
Step 2: Split the plots into two.
Step 3: Randomize the non-fixed or easy-to-change factor within each plot (in this example, that’s the fertilizer):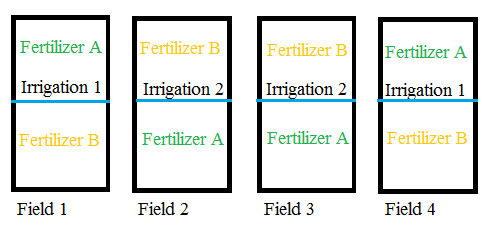
Compare the above image with one you might get from a complete randomization — where both the irrigation and fertilizer are randomly allocated between the 8 subplots: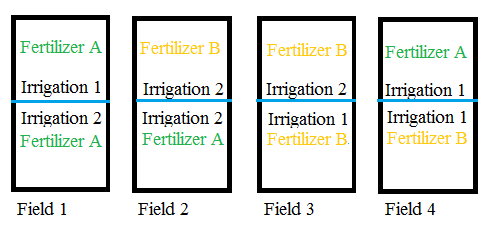
Advantages and Disadvantages
Compared to completely randomized designs, split-plot designs have the following advantages:
- Cheaper to run. In the above example, implementing a new irrigation method for each subplot would be extremely expensive.
- More efficient statistically, with increased precision.
This type of design does have many disadvantages, including:
- Implementing the design can be difficult, and requires advanced knowledge of a specific discipline (e.g. agriculture, factory production, or epidemiology). These designs are difficult to create and to spot– many published papers contain split-slot designs that are incorrectly classified and analyzed (Jones & Nachtsheim, 2009).
- Software packages that assist with the design are hard to find, although SAS and JMP have options.
Next: Split-Block Design
References
Box, G. and Meyer, R. D. (1986). Box, G.; Hunter, W.; and Hunter, S. (2005). Statistics for
Experimenters: Design, Innovation, and Discovery, 2nd edition. New York, NY: Wiley-Interscience.“An Analysis for Unreplicated Fractional Factorials”. Technometrics 28, pp. 11–18.
Fisher, R. A. (1925). Statistical Methods for Research Workers. Edinburgh: Oliver and Boyd.
Jones, B. & Nachtsheim, C. (2009). “Split-Splot Designs: What, Why, and How.” Journal of Quality Technology ,October.