Contents (Click to skip to that section):
- What is the Monty Hall Problem?
- A More Intuitive Way to Look at the Monty Hall Problem
- Why Does Switching Work?
- 1975 Version of The Monty Hall Problem
- The Media Furor
- Using Bayes’ Theorem to Solve the Monty Hall Problem
What is the Monty Hall Problem?
Watch the video for an overview:
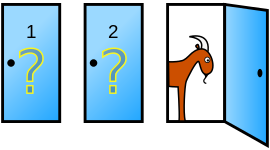
The Monty Hall problem is a probability puzzle named after Monty Hall, the original host of the TV show Let’s Make a Deal. It’s a famous paradox that has a solution that is so absurd, most people refuse to believe it’s true.
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? ~ (From Parade magazine’s Ask Marilyn column)
Should you Switch?
Believe it or not, it’s actually to your benefit to switch:
- If you switch, you have roughly a 2/3 chance of winning the car.
- If you stick to your original choice you have roughly a 1/3 chance of winning the car.
The answer sounds unlikely. After door 3 is opened, you would think that you then have two doors to choose from…both with the same odds. However, you are actually much more likely to win if you switch.
- Those who switched doors won about 2/3 of the time
- Those who didn’t switch won about 1/3 of the time
This fact has been proved over and over again with a plethora of mathematical simulations. If you’re stumped and still don’t believe it — don’t worry, even mathematicians scratch their head on this one. One genius mathematician, Paul Erdős didn’t believe the answer was right until he was shown simulations of the winning, “switch”, strategy.
Back to Top
A More Intuitive Way to Look at the Monty Hall Problem
A lot of people have trouble with the better odds of switching doors. Myself included, until I realized a simple fact: the odds are better if you switch because Monty curates the remaining choices. Let’s say you played the game where Monty doesn’t know the location of the car. It wouldn’t make any difference if you switch or not (your odds would be 50% no matter what). But this isn’t what happens. The Monty Hall problem has a very specific clause: Monty knows where the car is. He never chooses the door with the car. And by curating the remaining doors for you, he raises the odds that switching is always a good bet.
Another of the reasons some people can’t wrap their head around the Monty Hall problem is the small numbers. Let’s look at the exact same problem with 100 doors instead of 3. You pick a random door.

Instead of one door, Monty eliminates 98 doors.These are doors that he knows do not have the prize! This leaves two doors. The one you picked, and one that was left after Monty eliminated the others.

Do you switch doors now? You should. When you first picked, you only had a 1/100 chance of getting the right door. Furthermore, it was sheer guesswork. Now you’re being presented with a filtered choice, curated by Monty Hall himself. It should be clear that now your odds are much better if you switch.
Still don’t believe it? Try this simulation. You’ll see that if you switch, you’ll win about 2/3 of the time.
Back to Top
Why Does Switching Work?
Probably the best way to convince yourself that the solution is true is to try the simulation yourself.
Now, if you want to wrap your head around why it works, there are a couple of different ways to approach this. There are 3 doors and your original choice gives you odds of 1/3. There are two doors left, which have, together, a 2/3 chance of winning the car. Especially relevant is the fact that Monty opening one of those doors doesn’t change the odds. Those odds will still be 2/3.
Still not convinced? Imagine that instead of 3 doors, there are 300 doors. You guess door 1, which gives you a 1/300 chance of winning. Monty opens 298 out of the remaining doors, leaving you to choose between door 1 or door 201. While your original odds (1/300) remain the same for that randomly chosen door (door 1), Monty has given you increased odds by giving you the best door out of 298 randomly chosen doors. the best door out of a set of random doors will always have better odds.
Parade Magazine Solution
This solution, given in Parade Magazine, shows all of the possible results of staying or switching.

STAYING:
You pick door 1. Monty opens a “goat door.” You stay. For scenario 1, you would win. And for the other two scenarios you would lose. Giving you a 1/3 chance of winning for all scenarios.
SWITCHING
You pick door 1. Monty opens a “goat door.” You switch. For scenario 1 you would lose. And this time, for the other two scenarios you would win. This gives you 2/3 odds of winning.
Back to Top
1975 Version of The Monty Hall Problem
Although the problem was made famous in the Ask Marilyn column in 1990, the earliest mention of the problem was in a letter Steve Selvin wrote to the American Statistician. In his Letter to the Editor, called “A Problem in Probability,” Selvin posed the Monty Hall Problem. Instead of three doors, there were 3 boxes labeled A, B, and C. One contained the keys to a new Lincoln Continental. The other two boxes were empty. The contestant chooses a box, Monty opens an empty box, and he asks the contestant if he wants to switch. The question is pretty much the same, except instead of a car, doors and goats, you have a car, boxes and nothing. After posing the question (should the contestant switch?), Selvin provides the solution:

If you count the number of wins/losses in the “Result” column, you get 6/9, which is a probability of winning of 2/3.
Back to Top
The Media Furor
As to why this probability problem became so famous has a lot to do with the media furor that followed Marilyn’s answer in the Ask Marilyn column, which was:
“Yes; you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance. Here’s a good way to visualize what happened. Suppose there are a million doors, and you pick door #1. Then the host, who knows what’s behind the doors and will always avoid the one with the prize, opens them all except door #777,777. You’d switch to that door pretty fast, wouldn’t you?”
Disagreements with the Solution
Of the thousands of letters Marilyn received after the column was published, most disagreed with her.
A Few Comments
Here are a couple of comments (from Marilyn’s Game Show Problem page):
Robert Sachs, Ph.D. responded “As a professional mathematician, I’m very concerned with the general public’s lack of mathematical skills. Please help by confessing your error and in the future being more careful.”
Scott Smith, Ph.D.“You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I’ll explain…”
Barry Pasternack, Ph.D. Your answer to the question is in error. But if it is any consolation, many of my academic colleagues have also been stumped by this problem.
Marilyn posted a response, re-explaining her answer, which prompted even more letters begging her to correct her error. They include letters from the Deputy Director of the Center for Defense Information and a Research Mathematical Statistician from the National Institutes of Health. Marilyn appealed to math classrooms across the country to perform experiments to confirm the theory, and across the county classrooms were performing the probability experiment. Anyone who was in grade school in 1990 probably remembers the furor.
Try your own experiment at home…
Still don’t quite get the Monty Hall problem? Try your own experiment at home. Put a toy car under one of three boxes and play the game a hundred times yourself, noting your results. But with all of those Ph.D.s being wrong, don’t feel bad if you’re still stumped.
On the other hand, you can find comfort in the fact that pigeons may be smarter than mathematicians: they perform better when it comes to the Monty Hall Dilemma. A study published in the Journal of Comparative Psychology used a version of the game to dispense mixed grain as the prize. Birds did pretty well, better in fact, than their human counterparts. The experiment was repeated with people (although hopefully, with something other than grain for the prize…). Even after “extensive training,” the people still didn’t do as well as the birds. Food for thought!
More Reading…
The Monty Hall problem inspired thousands of websites, newspapers and other media to try and find their own answers to the problem. Google “Monty Hall Problem” and you’ll get several hundred thousand pages. Most state the problem, and offer solutions similar to what you read above. But there’s some pretty unique solutions out there if you know where to look:
Emory Law School professor Sasha Volokh, writing for The Washington Post, tackles the problem from a conditional probability perspective. If you’re comfortable with fairly advanced probability, this will make for an interesting read. “The true explanation is that Monty must show door 2 if the car is behind door 3, but he may show door 2 if the car is behind door 1, so his choice to show door 2 gives you a moderate amount of information in favor of the door-3 scenario.”
Mathematics Professor Jason Rosenhouse wrote an entire book on the subject called The Monty Hall Problem: The Remarkable Story of Math’s Most Contentious Brainteaser (Oxford University Press, 2009). In this book, he approaches the problem from a variety of perspectives from logical argument to mathematical rigor. He is (obviously) more thorough than even the most well-respecting we page could possibly be. You can find it on Amazon.
Using Bayes’ Theorem to Solve the Monty Hall Problem
The above “solutions” are logical solutions to the problem. A more rigorous solution can be found using Bayes’ Theorem. Credit goes to Christopher Long for this interesting solution. I’m going to assume that you are familiar with Bayes’ Theorem, which is a way to figure out conditional probability (if event A happens, what’s the probability event B will happen?).
The basis for the solution is the same as in the above scenario. There are three doors, one has the car behind it. You pick a door, then Monty opens one of the other doors to reveal a goat.
Let’s assume you pick door 1 and then Monty shows you the goat behind door 2. In order to use Bayes’ Theorem we need to first assign an event to A and B.
- Let event A be that the car is behind door number 1.
- Let event B be that Monty opens up door 2 to show the goat.
Here’s the Bayes’ solution
:
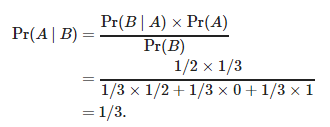
Pr(A) is pretty simple to figure out. There is a 1/3 chance that the car is behind door 1. There are two doors left, and each has a 1/2 chance of being chosen — which gives us Pr(B|A), or the probability of event B, given A.
Pr(B), in the denominator, is a little trickier to figure out. Consider that:
- You choose door 1. Monty shows you a goat behind door 2.
- If the car is behind door 1, Monty will not choose it. He’ll open door 2 and show a goat 1/2 of the time.
- If the car is behind door 2, Monty will always open door 3, as he never reveals the car.
- If the car is behind door 3, Monty will open door 2 100% of the time.
As Monty has opened door 2, you know the car is either behind door 1 (your choice) or door 3. The probability of the car being behind door 1 is 1/3. This means that the probability of the car being behind door 3 is 1 – (1/3) = 2/3. And that is why you switch.
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company