A linear operator is a function that maps one vector onto other vectors. They can be represented by matrices, which can be thought of as coordinate representations of linear operators (Hjortso & Wolenski, 2008). Therefore, any n x m matrix is an example of a linear operator.
An example of an operator that isn’t linear: Gα = α2.
Formal Definition
A linear operator is usually (but not always) defined to satisfy the conditions of additivity and multiplicativity.
- Additivity: f(x + y) = f(x) + f(y) for all x and y,
- Multiplicativity: f(cx) = cf(x) for all x and all constants c.
More formally, a linear operator can be defined as a mapping A from X to Y, if:
for all x and y in the domain of A and α, β ∈ &Copf (Hanson & Yakolev, 2002).
In quantum mechanics, a linear operator still satisfies the additivity and multiplicativity conditions, but is defined in terms of wavelengths ![]() (Branson, 2013):
(Branson, 2013):
![]()
Linear Operator Examples
The simplest linear operator is the identity operator, 1; It multiplies a vector by the scalar 1, leaving any vector unchanged. Another example: a scalar multiple b · 1 (usually written as just b), which multiplies a vector by the scalar b (Jordan, 2012). In fact, any multiplicative constant is also a simple linear operator.
Tensors are a type of linear operator frequently encountered in engineering and physics. In calculus, differential operators are linear operators (Branson, 2013), although they usually aren’t referred to as such in a basic calculus class. The formal rule above can be written in terms of a derivative:
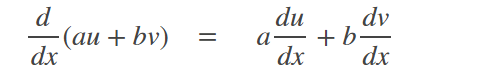
And an integral:
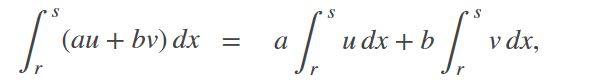
References
Hanson, G. & Yakolev, A. (2012). Operator Theory for Magnetics: an introduction. Springer.
Hjortso, M. & Wolenski, P. (2008). Linear Mathematical Models in Chemical Engineering. World Scientific Publishing Company.
Jordan, T. (2012). Linear Operators for Quantum Mechanics. Dover Publications.