A loop is just an edge that joins a node to itself; so a Hamiltonian cycle is a path traveling from a point back to itself, visiting every node en route.
If a graph with more than one node (i.e. a non-singleton graph) has this type of cycle, we call it a Hamiltonian graph.
There isn’t any equation or general trick to finding out whether a graph has a Hamiltonian cycle; the only way to determine this is to do a complete and exhaustive search, going through all the options.
History of the Hamiltonian Cycle
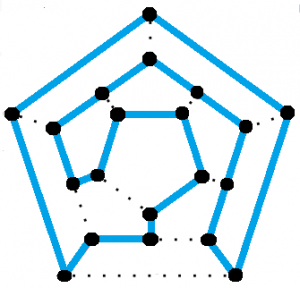
The cycle was named after Sir William Rowan Hamilton who, in 1857, invented a puzzle-game which involved hunting for a Hamiltonian cycle. The game, called the Icosian game, was distributed as a dodecahedron graph with a hole at each vertex. To solve the puzzle or win the game one had to use pegs and string to find the Hamiltonian cycle — a closed loop that visited every hole exactly once. The solution is shown in the image above.
Examples of Hamiltonian Graphs
Every complete graph with more than two vertices is a Hamiltonian graph. This follows from the definition of a complete graph: an undirected, simple graph such that every pair of nodes is connected by a unique edge.
The graph of every platonic solid is a Hamiltonian graph. So the graph of a cube, a tetrahedron, an octahedron, or an icosahedron are all Hamiltonian graphs with Hamiltonian cycles.
A graph with n vertices (where n > 3) is Hamiltonian if the sum of the degrees of every pair of non-adjacent vertices is n or greater. This is known as Ore’s theorem.
Applications of Hamiltonian cycles and Graphs
A search for these cycles isn’t just a fun game for the afternoon off. It has real applications in such diverse fields as computer graphics, electronic circuit design, mapping genomes, and operations research.
For instance, when mapping genomes scientists must combine many tiny fragments of genetic code (“reads”, they are called), into one single genomic sequence (a ‘superstring’). This can be done by finding a Hamiltonian path or cycle, where each of the reads are considered nodes in a graph and each overlap (place where the end of one read matches the beginning of another) is considered to be an edge.
In a much less complex application of exactly the same math, school districts use Hamiltonians to plan the best route to pick up students from across the district. Here students may be considered nodes, the paths between them edges, and the bus wishes to travel a route that will pass each students house exactly once.
References
Icosian Game
On Hamiltonian Cycles and Hamiltonian Paths
Genome Assembly
Graph Algorithms in Bioinformatics