A frequency distribution table in Excel gives you a snapshot of how your data is spread out. It’s usual to pair a frequency distribution table with a histogram. A histogram gives you a graph to go with the table. In order to make a frequency distribution table in Excel with a histogram, you must have the Data Analysis Toolpak installed.
Watch the video for the steps:
Example Problem: Make a frequency distribution table in Excel. Use the following IQ scores: 99, 101, 121, 132, 140, 155, 98, 90, 100, 111, 115, 116, 121, 124.
Step 1: Type your data into a worksheet. Make sure you put your data into columns. Use column headers. For this example, type “IQ Scores” into cell A1. Then type the IQ scores into cells A2 to A15. Note: Column headers will become the labels on the histogram.
Step 2: Type the upper levels for your BINs into a separate column. For this sample problem, type 99, 109, 119, 129, 139, and 149 as your upper limits into column C. Note that I “missed” the top value of 155. You’ll see what Excel does with the “outlier” in the last step.
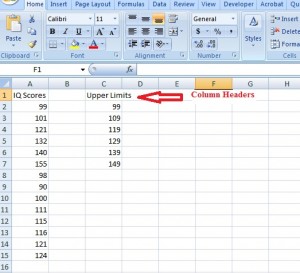
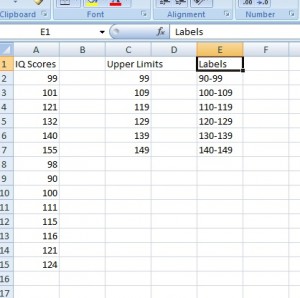
Step 3: Make a column of labels so it’s clear what BINs the upper limits are labels for.
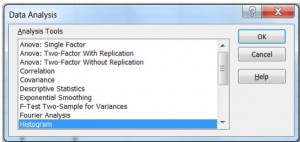
Step 4: Click the “Data” tab. Then click “Data Analysis”. If you don’t see data analysis, make sure you have installed the Data Analysis Toolpak.
Step 5: Click “Histogram” and then click “OK.”
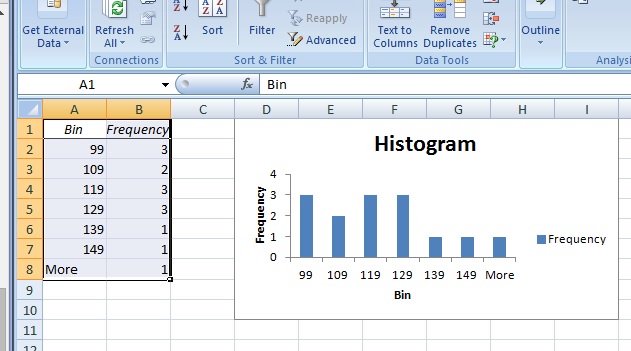
Step 6: Type where your data is into the “Input Range” text box. For this sample problem, type “A2:A15”.
Step 7: Type where your upper limits are into the “BIN Range” text box. For this sample problem, type “C2:C7”.
Step 8: Select a location where you want your output to appear. For example, click the “New Worksheet” button.
Step 9: Click “Chart Output” and then click “OK.” Excel will put the histogram next to your frequency table. Note that the item I missed (155) has been magically inserted into the chart (in the BIN labeled “More”). Of course, if you want this upper BIN to be labeled, you can always add a new BIN (150-159) and redo the chart!
That’s it!
Tip: How many different BINs you have is up to you. Most tables have around 5 to 10. Make sure your BINs include all of your lower values and all of your upper values.
Check out our YouTube channel for more Excel/Stats videos!
References
Salkind, N. (2016). Statistics for People Who (Think They) Hate Statistics: Using Microsoft Excel 4th Edition.