What is a Plackett-Burman Design?
A Plackett-Burman design (a type of screening design) helps you to find out which factors in an experiment are important. This design screens out unimportant factors (noise), which means that you avoid collecting large amounts of data on relatively unimportant factors.
For example, dozens of factors contribute to lung cancer, including:
- Number of cigarettes smoked per day.
- Second-hand smoke.
- Years smoking cigarettes.
- Genetics.
- Cadmium.
- Chromium.
- Nickel.
- Uranium.
- Plutonium-239.
- X-rays.
- Gamma Radiation.
- Beta-carotene supplements.
- Coal-tar pitch.
- Soot.
- Diesel Engine Exhaust.
- Paint fumes.
- Emissions from high temperature frying.
- Burning wood indoors.
- Burning coal indoors.
- Radon.
- Asbestos.
- Silica dust, crystalline.
- Bis(chloromethyl)ether; chloromethyl methyl ether
- Sulfur Mustard.
- Aluminum production.
- Coal gasification.
- Coke production.
- Hematite mining.
- Iron and Steel founding.
- Rubber production industry.
- MOPP (vincristine-prednisone-nitrogen mustard-procarbazine mixture).
If you are doing a study of, say, lung cancer in South Florida residents, some factors (like cigarette smoking) are more important than others (like hematite mining). The Plackett-Burman would help you to screen out the least important factors.
Number of Factors
The Plackett-Burman design can only be used for experiments that are multiples of 4 with 8 as the starting point (N = 8, 12, 16, 20, 24, 28, 32, 36). A minimum of 4n experiments is needed for estimating main effects for 4n-1 factors (Plackett & Burman, 1946). For example, 4, 5, 6, or 7 factors would require 8 experimental runs, 8, 9, 10, or 11 would require 12 runs, and so on.
Designing Plackett-Burman Experiments by Hand
Programs like Minitab and JMP can calculate the runs automatically. Tables are also available (from which the software programs are based). By hand, they are easy to construct (from Rekab & Shaikh):
Step 1: Choose a generating vector from the following list: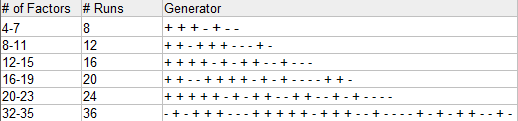
For this example, I have 7 factors A B C D E F G, so the generating vector is in the first row.
Step 2: Assign the generating vector to the first factor (factor A in this example). Add a “-” as a final entry to complete the quartets (in this example, the “-” would be the 8th entry):
Step 3: Copy the seventh entry for the first factor, A, to the first entry in B. Slide all of the factors in A down (note: ignore the final column we filled in: just carry the “-” across all columns):

Step 4: Repeat Step 3, shifting down for each column until the table is completed.
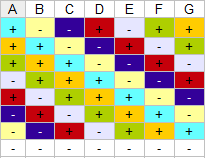
Advantages and Disadvantages
A Plackett-Burman Design can help you sort out which factors to concentrate on, greatly reducing the amount of data you have to collect. For example, if you have 15 factors in your design, you can work with as few as 20 data points in a Plackett-Burman. A full factorial design would require over a thousand times that amount (32,768 data points). That said, working with few data points means that you can’t really say for sure what any effects are in an experiment, nor can you tell which factors have effects on other factors. Therefore, the Plackett-Burman should be used as a starting point for further experiments. Once you’ve identified the important factors, you can run a full factorial or fractional design to study those factors more.
References:
CDC: What Are the Risk Factors for Lung Cancer?
Occupational and Environmental Causes of Lung Cancer.
Statistical Design of Experiments with Engineering ApplicationsBy Kamel Rekab, Muzaffar Shaikh