Statistics Definitions > Internal Consistency Reliability
What is Internal Consistency Reliability?
Internal consistency reliability is a way to gauge how well a test or survey is actually measuring what you want it to measure.
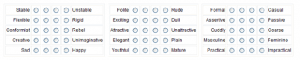
A simple example: you want to find out how satisfied your customers are with the level of customer service they receive at your call center. You send out a survey with three questions designed to measure overall satisfaction. Choices for each question are: Strongly agree/Agree/Neutral/Disagree/Strongly disagree.
- I was satisfied with my experience.
- I will probably recommend your company to others.
- If I write an online review, it would be positive.
If the survey has good internal consistency, respondents should answer the same for each question, i.e. three “agrees” or three “strongly disagrees.” If different answers are given, this is a sign that your questions are poorly worded and are not reliably measuring customer satisfaction. Most researchers prefer to include at least two questions that measure the same thing (the above survey has three).
Another example: you give students a math test for number sense and logic. High internal consistency would tell you that the test is measuring those constructs well. Low internal consistency means that your math test is testing something else (like arithmetic skills) instead of, or in addition to, number sense and logic.
Testing for Internal Consistency
In order to test for internal consistency, you should send out the surveys at the same time. Sending the surveys out over different periods of time, while testing, could introduce confounding variables.
An informal way to test for internal consistency is just to compare the answers to see if they all agree with each other. In real life, you will likely get a wide variety of answers, making it difficult to see if internal consistency is good or not. A wide variety of statistical tests are available for internal consistency; one of the most widely used is Cronbach’s Alpha.
- Average inter-item correlation finds the average of all correlations between pairs of questions.
- Split Half Reliability: all items that measure the same thing are randomly split into two. The two halves of the test are given to a group of people and find the correlation between the two. The split-half reliability is the correlation between the two sets of scores.
- Kuder-Richardson 20: the higher the Kuder-Richardson score (from 0 to 1), the stronger the relationship between test items. A Score of at least 70 is considered good reliability.
Next: Cronbach’s Alpha
References:
How do I interpret my test results? April 2010. Retrievd 2/26/2016 from http://academicdepartments.musc.edu/appletree/brown_bag/brown_bag_files/2010/lancaster_appletree_4_10.pdf