Watch the video, or read the article below:
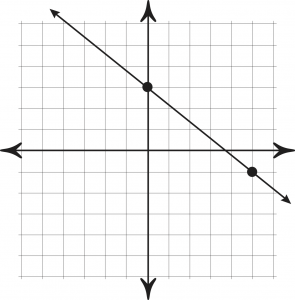
In an introductory stats class, one of the first things you’ll learn is the difference between discrete vs continuous variables. In a nutshell, discrete variables are points plotted on a chart and a continuous variable can be plotted as a line.
Discrete vs Continuous variables: Definitions.
What is a Discrete Variable?
Discrete variables are countable in a finite amount of time. For example, you can count the change in your pocket. You can count the money in your bank account. You could also count the amount of money in everyone’s bank accounts. It might take you a long time to count that last item, but the point is—it’s still countable.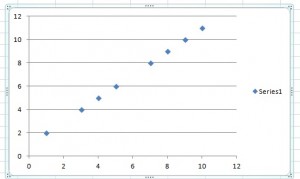
What is a Continuous Variable?
Continuous Variables would (literally) take forever to count. In fact, you would get to “forever” and never finish counting them. For example, take age. You can’t count “age”. Why not? Because it would literally take forever. For example, you could be:
25 years, 10 months, 2 days, 5 hours, 4 seconds, 4 milliseconds, 8 nanoseconds, 99 picosends…and so on.

You could turn age into a discrete variable and then you could count it. For example:
- A person’s age in years.
- A baby’s age in months.
Take a look at this article on orders of magnitude of time and you’ll see why time or age just isn’t countable. Try counting your age in Planctoseconds (good luck…see you at the end of time!).
Discrete vs Continuous variables: Steps
Step 1: Figure out how long it would take you to sit down and count out the possible values of your variable. For example, if your variable is “Temperature in Arizona,” how long would it take you to write every possible temperature? It would take you literally forever:
50°, 50.1°, 50.11°, 50.111°, 50.1111°, …
If you start counting now and never, ever, ever finish (i.e. the numbers go on and on until infinity), you have what’s called a continuous variable.
If your variable is “Number of Planets around a star,” then you can count all of the numbers out (there can’t be an infinite number of planets). That is a discrete variable.
Step 2: Think about “hidden” numbers that you haven’t considered. For example: is time a discrete or continuous variable? You might think it’s continuous (after all, time goes on forever, right?) but if we’re thinking about numbers on a wristwatch (or a stop watch), those numbers are limited by the numbers or number of decimal places that a manufacturer has decided to put into the watch. It’s unlikely that you’ll be given an ambiguous question like this in your elementary stats class but it’s worth thinking about!
Check out our Youtube channel for more stats tips and help!
References
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 927 and 929, 1972.