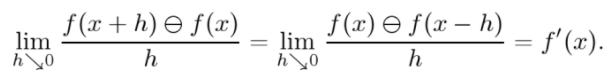Derivatives > Hukuhara derivative
Generalized Hukuhara differentiability is the most general type of differentiability for interval-valued functions [1]. Hukuhara introduced the idea of the Hukahara derivative (H-Derivative) in his 1967 paper [2], which became a starting point for the study of set differential equations and fuzzy differential equations [3].
Hukuhara Derivative: Definition
Hukuhara first described the Hukahara derivative of f at x as the fuzzy number (an imprecise number) f′(x), defined as:
A function f: (a, b) → ℝF is Hukahara differentiable if, for sufficiently small h > 0, the H-differences
f (x + h) ⊖ f(x) and f(x) ⊖ f(x – h) exist and if there is also an element f′(x) ∈ ℝF such that [4]:
Hukuhara defined the “H-difference” to overcome the problem of finding a suitable difference between two intervals for interval-valued functions:
- If A = B + C, then the H-difference is A and B (denoted by A – HB) equals C.
- For arbitrary pairs of intervals, the H-difference may or may not exist [3].
Generalized Hukuhara Derivative
The “classical” Hukuhara derivative from Hukuhara’s paper has a shortcoming: solutions for interval differential equations (IDEs), which are interval-valued mappings, have values with non-decreasing length. This means that the uncertainty shown by the solutions grows over time [5]. This “new” version (the generalized Hukuhara derivative) removed the problem of these time-sensitive, imprecise solutions.
Stefanini and Bede’s [6] research on interval differential equations introduced a new version of the Hukuhara derivative for interval-valued mappings. Their approach has solutions where values have non-increasing length.
The H-Difference
Hukuhara defined a new difference for compact and convex sets. The Hukuhara difference (H-difference), a special case of the Minkowski difference, is one way to handle the inverse element problem for compact and convex sets. The inverse element drawback describes how convex sets have a linear structure with respect to Minkowski sum and scalar multiplication. This structure is a cone instead of a vector, because the inverse element of a set (with respect to the Minkowski sum) may not exist. To put this another way, if A = {a} isn’t a singleton set, the Minkowski sum of A and −A may not be the identity element {0}—. In other words, A + (−1)A ≠ {0}. Hukuhara’s studies also led to the development of the H-difference of fuzzy sets and fuzzy number-valued functions.[7].
References
[1] Cano, Y. et al. (2012). Calculus for interval-valued functions using generalized Hukuhara derivative and applications. Retrieved November 23, 2021 from: https://www.sciencedirect.com/science/article/abs/pii/S016501141200509X
[2] M. Hukuhara, Intégration des applications mesurables dont la valeur est un compact convexe, Funkcial. Ekvac. 10 (1967) 205–223.
[3] Cano, Y. et al. Calculus for interval-valued functions using generalized Hukuhara
derivative and applications. Fuzzy Sets and Systems 219 (2013) 49–67.
[4] Bede, B. (2012). Mathematics of Fuzzy Sets and Fuzzy Logic. Springer Berlin Heidelberg.
[5] Malinowski, M. Interval differential equations with a second type Hukuhara derivative. Retrieved November 23, 2021 from: https://core.ac.uk/download/pdf/82239432.pdf
[6] L. Stefanini, B. Bede, Generalized Hukuhara differentiability of interval-valued functions and interval differential equations, Nonlinear Anal. 71 (2009)
1311–1328.
[7] Okin, A. & Bayeg, S.The concept of Hukuhara derivative and Aumann integral for intuitionistic fuzzy number valued functions. MANAS Journal of Engineering MJEN Volume 6 (Issue 2) (2018) Pages 143-163.