Hoeffding’s inequality is useful for bounding quantities that are hard to compute. It gives an upper bound on the probability that the sum of a set of random variables deviates from the expected value.
In layman’s terms, lets say we have a set of variables. When we find the average, we should usually get a result that’s close to the expected value. Hoeffding’s inequality formally states what this “close” and “usually” should be [1].
Although the inequality is a general result in probability theory, it is widely used in machine learning as well as more esoteric topics such as information theory, random algorithm analysis, and statistical learning theory.
Hoeffding’s inequality definition
There are several equivalent forms of Hoeffding’s inequality. One common one is:
Suppose that random variables X1, … , Xn are independent. In addition, ai ≤ Xi ≤ bi, and E[Xi] = µ. Then, for any t > 0,
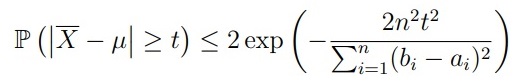
Where
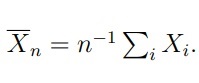
When a ≤ Xi ≤ b the formula becomes [2]:
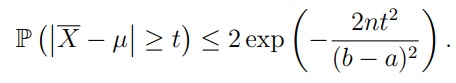
Relationship to Other Inequalities
Hoeffding’s inequality is a special case of the Azuma–Hoeffding inequality, a basic concentration inequality (inequalities that bound probabilities of deviations by a random variable from its mean or median) where the deviation probabilities decay exponentially or superexponentially — faster than exponentially — in distance from the mean.
It is also a special case of McDiarmid’s inequality, which also shows how the values of a bounded function of independent random variables are concentrated about the mean. However, while Hoeffding’s focuses on sums of random variables, McDiarmid’s inequalitycan be extended to more general functions [3].
It is similar to the Chernoff bound, but tends to be less sharp, in particular when the variance of the random variables is small.[2] It is similar to, but incomparable with, one of Bernstein’s inequalities.
References
[1] Donke, J. Learning Theory. Statistical Machine Learning.
[2] Wasserman, L. Hoeffding’s inequality. Retrieved July 27, 2022 from: https://www.stat.cmu.edu/~larry/=stat700/Lecture6.pdf
[3] Concentration of Measure.