Contents:
Definition
An integer includes whole numbers and negative whole numbers. Integers can be positive, negative, or zero. For example: 1, -1, 0, 101 and -101.
The set of integers is often given the symbol Z, and Z is defined as
{…, -3, -2,-1, 0, 1, 2, 3,…}
There are an infinite number of integers. They can be ordered by being placed on a number line; the number to the right is always greater than the one to the left.
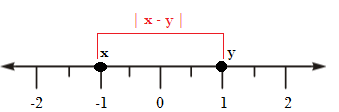
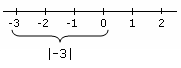
Absolute Value of an Integer
The absolute value of an integer is the distance from that number to the origin (0). Since both 3 and -3 are 3 units (steps) away from the origin, the absolute value of both numbers is 3.
Sign
The sign (-) for all integers to the left of the origin (0) is (-) and for all numbers to the right (+). Negative integers are those with a (-) sign and positive ones are those with a (+) sign. Positive integers may be written without their sign.
Addition and Subtractions
To add two integers with the same sign, add the absolute values and give the sum the same sign as both values.
For example: (-4) + (-7) = -(4 + 7)= – 11.
To add two integers with different signs, find the difference in absolute values and give the difference the same sign as the number with the largest absolute value.
For example: (-5) + (3)
- Find the absolute values (5 and 3).
- Find the difference between 5 and 3 (5 – 3 = 2).
- Find the sign of the largest absolute value. -5 has a negative sign.
- Add the sign from Step 3 to the difference you found in Step 2. The result is -2.
Subtracting means adding its opposite.
For example:
Subtracting -2 from 10, we get:
10 – – 2 = 10 + 2 (2 is the opposite of -2) = 12.
Subtracting 2 from 10 we get:
10 + (-2) = 8.
When an integer is added to or subtracted by another, the result is always an integer.
Multiplication
To multiply an integer, multiply the absolute value. If the two integers being multiplied have the same sign, the result is positive. If the two integers have different signs, the result is negative.
When one integer is multiplied by another, the result is always an integer. But when one is divided by another the result may or may not be an integer. For example, while 3/3 = 1 and 8/4 = 2 and are integers, 3/4 and 8/5 are not.
Integer Programming
Integer programming (IP) problems are a type of feasibility or mathematical optimization problem where some (or all) of the variables are restricted to integer values.
- If all variables are restricted to integers, the IP problem is called a pure integer programming (IP) problem.
- If variables are a mixture between required integers and others wit no such restriction, the IP problem is called a mixed IP problem.
- If the integers are restricted to 0 or 1, the problem is called a pure—or mixed&mdas;binary integer programming problem.
Sometimes the term IP is used to refer to integer linear programming, a type of programming where both the objective function and any non-integer constraints are linear.
Modeling with IP Problems
When are IP problems used, though? Often to model real life problems, where values are naturally restricted to integers. For example, if we modeled computer production in a factory in China with simple linear programming models, we might come up with a plan of 2067.4 computers per month. That “.4” doesn’t make intuitive sense; how can a factory produce 40% of a computer (although I suppose they could halt the line when that .4 of a computer is finished!). We could round it, but would prefer if it was an integer in the first place.
Sometimes non-integer variables make even less sense. For example, a linear programming model assigning teachers to particular cities to might recommend placing 0.7 teachers in one town and 0.5 in another. We need a way of making models that accounts for the integers of some or all variables.
Formulating and Solving IP Problems
Formulating IPs are typically more difficult than formulating simple linear programs. Though there are some tricks, the key is practice.
There are no general purpose, computational effective algorithms for solving IPs analogous to those used for linear programs. Instead, you must usually choose between general purpose, computationally ineffective solution methods or design a special purpose algorithm that can attack just this specific problem.
References
- MathWorks, Inc. IP. Retrieved from
https://www.mathworks.com/discovery/integer-programming.html on May 5, 2018. - IBM Knowledge Center. What is IP? Retrieved from https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.1/ilog.odms.ide.help/OPL_Studio/opllanguser/topics/opl_languser_shortTour_IP_what.html on May 5, 2018
- Beasley, J E. Operations Research Notes: Programming. Retrieved from http://people.brunel.ac.uk/~mastjjb/jeb/or/ip.html on May 5, 2018
- Positive and Negative. http://web.cerritos.edu/dford/SitePages/Math_40/Math40Lesson6.pdf. Retrieved June 19, 2018
- Dvorscak, B. Adding and Subtracting. https://mypages.iit.edu/~smart/dvorber/lesson4.htm Retrieved June 19, 2018