Statistics Definitions > Item Response Theory
What is Item Response Theory?
Item response Theory(IRT) is a way to analyze responses to tests or questionnaires with the goal of improving measurement accuracy and reliability. If you want your test to actually measure what it is supposed to measure (i.e. mathematical ability, a student’s reading ability or historical knowledge), IRT is one way to develop your tests.
The first step in IRT is the development of a two-dimensional matrix, which lists examinees and correct responses. In this matrix, 1 represents a correct answer and 0 an incorrect answer:
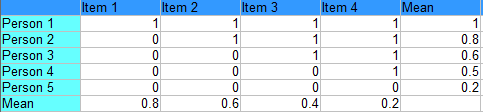
A quick look at this table tells you that person 1 answered all 5 questions correctly (100% proficient) while person 4 answered 2 questions (40% proficiency). However, proficiency isn’t the only factor in IRT theory: you must also take into account question difficulty. Let’s say you had two test takers who both get 2/5. The first test taker may have answered two easy questions, and the second test taker may have answered two difficult questions. Therefore, although they both scored 40%, their proficiency is not the same.
Item response theory takes into account the number of questions answered correctly and the difficulty of the question. The SAT and GRE both used Item Response Theory for their tests.
There are many different models for IRT. Three of the most popular are:
- The Rasch model,
- Two-parameter model,
- Graded Response model.
Some schools of thought consider the Rasch model as being completely separate from IRT. This is mainly because the Rasch model uses only a single parameter (called a “threshold”), while general IRT models use three. Another reason is that IRT aims to fit a model to data, while The Rasch model fits data to a model. Despite these differences, both models are used in favor of Classical Test Theory — where test taker’s scores vary from one test to another.
Next: Graded Response Model