The Kent distribution, also known as the 5-parameter Fisher-Bingham distribution, is a probability distribution in ℜ3, the real three dimensional coordinate space, of a two-dimensional unit sphere.
Kent Distribution PDF
The Kent distribution’s probability density function, f(x), is given by the equation:
![]()
Here,
- x is a three dimensional unit value.
- c(κ, β) is a normalizing constant, and is given by the equation
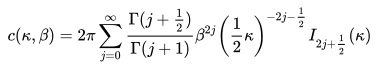
In the above equation, Iv(κ) represents what is called the modified Bessel function.
References
Boomsma, W., et al. (2006) Graphical models and directional statistics capture protein structure. In S. Barber, P.D. Baxter, K.V.Mardia, & R.E. Walls (Eds.), Interdisciplinary Statistics and Bioinformatics, pp. 91–94. Leeds, Leeds University Press.
Kent, J. T. (1982) The Fisher–Bingham distribution on the sphere., J. Royal. Stat. Soc., 44:71–80.
Mardia, K. V. M., Jupp, P. E. (2000) Directional Statistics (2nd edition), John Wiley and Sons Ltd