Z Interval: Simple Definition, Formula & Worked Example

“Z-interval” could refer to either:

A specific type of confidence interval (see below), or
A TI-83 calculator option to find a confidence interval for the mean using the Z Interval. If you’re using the TI-83, see this article on confidence intervals for step by step TI-83 Z Interval instructions.

You may want to read this article first: What is a confidence interval?

What is a Z Interval?

A z interval is a specific type of confidence interval which tells you a range where you can expect a particular mean or proportion to fall. It can be calculated from a known standard deviation.

Z-Interval vs. T-Interval

In general, you want to choose to calculate z-intervals when:

Your sample size is 30 or greater,
You know the standard deviation of your sample.

When you don’t know the standard deviation and still want to find a confidence interval, calculate a t-interval instead. The concept is the same, except that you use a different table to calculate the interval: the z-table for a z-interval and a t-table for a t-interval. For more on the specific differences between the “T” and “Z”, see: T-scores vs. Z-scores.

How to Calculate the Z Interval

Need help with a homework question? Check out our tutoring page!

A z interval for a mean is given by the formula:

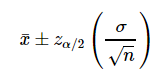
The formula may look a little daunting, but the individual parts are fairly easy to find:

n is the sample size.
σ is the standard deviation.
x̄ is the sample mean
z_α/2 is an alpha level’s z-score for a two tailed test (see note below).

Note: If z_α/2 is new to you, read all about z_α/2 here. Most of the time, you won’t have to do any calculations because the most common values are already known:

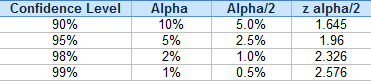
For example, if you’re trying to find a z-interval with a 90% confidence level and a 5% alpha (significance) level, then use 1.645 in the above equation.

Example

Suppose we want to calculate a 95 percent confidence interval for a situation where we know:

Mean (μ) = 50,
Standard deviation = 5,
Number of data points in the sample is 81.

For a 95 % confidence interval, the above table tells us that z_0.025 = 1.96.

Now we have all the data to plug into our formula, and our confidence interval will be:

[50- (1.96) (5/9), 50 + (1.96)(5/9)]

We can simplify this to:

[48.91, 51.09]

which is our confidence interval or z interval.

References

Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Pennsylvania State University Department of Statistics Online Programs. STAT 414 Intro Probability Theory. Lesson 30 Confidence Intervals for One Mean. Retrieved from https://newonlinecourses.science.psu.edu/stat414/node/194/ and https://newonlinecourses.science.psu.edu/stat414/node/196/ on May 30, 2018.
Walker, Jerimi Ann. Confidence Intervals for the Mean- By Hand. Retrieved from
https://www.mathbootcamps.com/calculating-confidence-intervals-for-the-mean/ on May 30, 2018.Xie, Yao. Lecture Notes: Confidence Interval. Retrieved from https://www2.isye.gatech.edu/~yxie77/isye2028/lecture7.pdf on May 30, 2018.