What is Z Alpha/2?
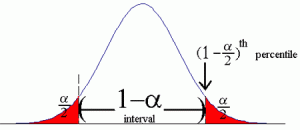
If you have a question asking you to find z alpha/2, you’re being asked to find an alpha level’s z-score for a two tailed test.
Alpha levels are related to confidence levels: to find alpha, just subtract the confidence interval from 100%. for example, the alpha level for a 90% confidence level is 100% – 90% = 10%.
To find alpha/2, divide the alpha level by 2. For example, if you have a 10% alpha level then alpha/2 is 5%.
How to find z α/2
You have three main options:
- Use known values for z alpha/2.
- Use a z-table.
- Use the TI-83/84.
Need help with a homework question? Check out our tutoring page!
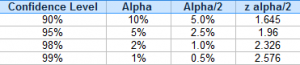
1. (Easiest Way) Use known values for z alpha/2.
You don’t actually have to look up z alpha/2 in a z-table every time. For most hypothesis tests, you’ll probably be using one of four confidence levels (90%, 95%, 98% and 99%). The z alpha/2 for each confidence level is always the same:
2. Use a Z-Table
Step 1: Find the alpha level. If you are given the alpha level in the question (for example, an alpha level of 10%), skip to step 2. Subtract your confidence level from 100%. For example, if you have a 95 percent confidence level, then 100% – 95% = 5%.
Step 2: Divide the amount you found in Step 1 by 2 to get the alpha level for a two-tailed test:
.50/2 = 2.5 percent.
Step 3: Subtract Step 2 from 50%:
50% – 2.5% = 47.5%
Step 4: Convert Step 3 to a decimal and find that area in the center of the z-table.
The closest z-score to 47.5 percent (.475) is at z=1.96.
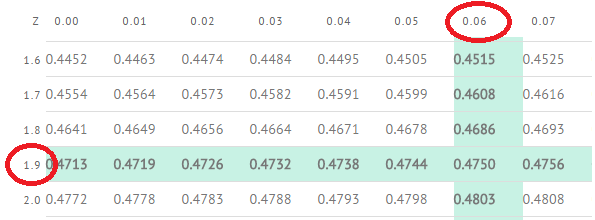
Note: This step depends on using the right-hand z-table on this site. There are several different possible z-table layouts, so you may get a different answer if you use a different z-table. I would suggest using the same z-table when learning how to look up areas/z-scores until you get the hang of it…then you should be able to use any z-table you come across.
TI-83 / TI-84
Step 1: Press “2nd” and then press “VARS”.
Step 2: Select “invNorm” and then press “ENTER.”
Step 3: Type in the percentage for alpha/2 from the above table. For example, type in 0.005 for a 99% confidence level.
Step 4: Type a closing parentheses “)” and then press ENTER.
The result will be the z-score for the left tail (in this example, -2.576). As the normal distribution curve is symmetrical, the cutoff for the right tail is the opposite: 2.576.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.