Probability Distributions > Uniform Distribution
Contents:
- What is a Uniform Distribution?
- Expected Value/Mean and Variance.
1. What is a Uniform Distribution?
A uniform distribution, also called a rectangular distribution, is a probability distribution that has constant probability.
This distribution is defined by two parameters, a and b:
- a is the minimum.
- b is the maximum.
The distribution is written as U(a, b).
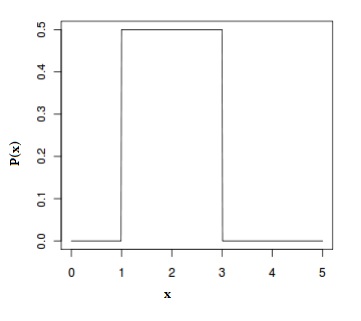
The following graph shows the distribution with a = 1 and b = 3:
Like all probability distributions for continuous random variables, the area under the graph of a random variable is always equal to 1. In the above graph, the area is:
A = l x h = 2 * 0.5 = 1.
Watch the video for an overview and a few worked examples:
Note: In actuarial science, the uniform distribution is called the de Moivre distribution.
Types
This distribution has two types. The most common type you’ll find in elementary statistics is the continuous uniform distribution (in the shape of a rectangle). However, there is a second type: the discrete uniform distribution. It still resembles a rectangle but instead of a line, a series of dots represent a known, finite number of outcomes. The following graph shows 5 possible outcomes:
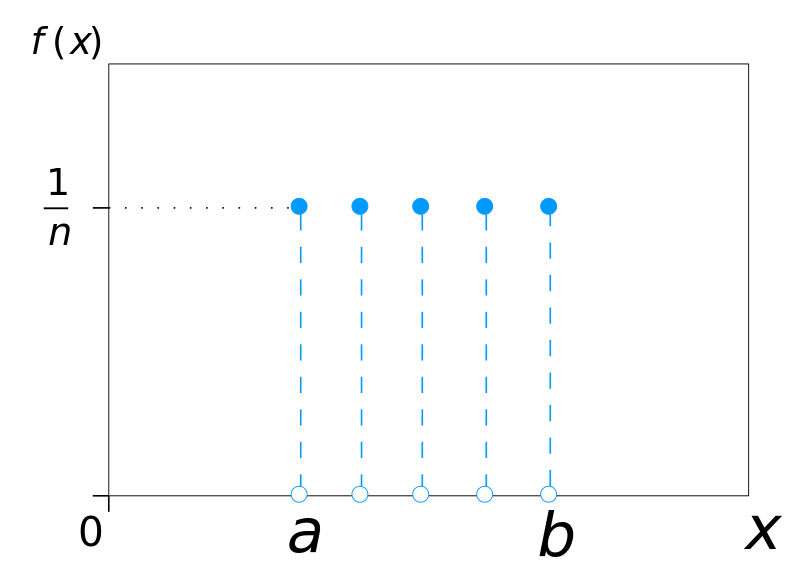
Rolling a single die is one example of a discrete uniform distribution; a die roll has four possible outcomes: 1,2,3,4,5, or 6. There is a 1/6 probability for each number being rolled.
General Formula
The general formula for the probability density function (pdf) for the uniform distribution is:
f(x) = 1/ (B-A) for A≤ x ≤B.
“A” is the location parameter: The location parameter tells you where the center of the graph is. “B” is the scale parameter: The scale parameter stretches the graph out on the horizontal axis. Note: The A and B here aren’t to be confused with lowercase (a,b), which is an open interval.
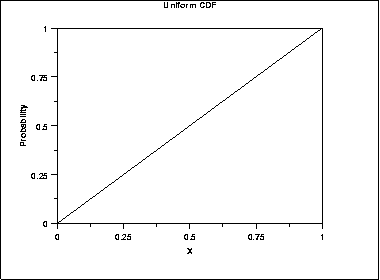
Uniform CDF
The uniform distribution doesn’t always look like a rectangle. A special case, the uniform cumulative distribution function, adds up all of the probabilities (in the same way a cumulative frequency distribution adds probabilities) and plots the result, which is a linear graph and not a rectangle:
Variables
The variables in a uniform distribution are called uniform random variables.
2. Expected Value and Variance.
The expected value (i.e. the mean) of a uniform random variable X is:
E(X) = (1/2) (a + b)
This is also written equivalently as:
E(X) = (b + a) / 2.
“a” in the formula is the minimum value in the distribution, and “b” is the maximum value.
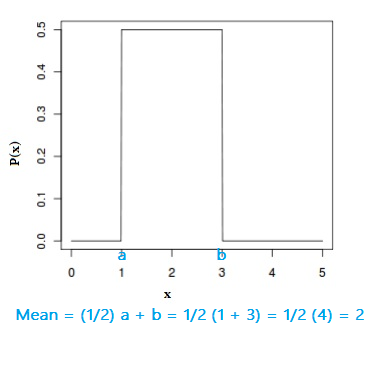
The variance of a uniform random variable is:
Var(x) = (1/12)(b-a)2
For the above image, the variance is (1/12)(3 – 1)2= 1/12 * 4 = 1/3.
3. Finding Probabilities for a Continuous Uniform Distribution
Need help with a homework question? Check out our tutoring page!
Example question #1: The average amount of weight gained by a person over the winter months is uniformly distributed from 0 to 30lbs. Find the probability a person will gain between 10 and 15lbs during the winter months.

Step 1: Find the height of the distribution. The area under a probability distribution is always 1. As there are 30 units (from zero to 30), then the height is 1/30.
Step 2: Find the width of the “slice” of the distribution mentioned in the question. Do this by subtracting the biggest number (b) from the smallest (a), to get b – a = 15 – 10 = 5.
Step 3: Multiply the width (Step 2) by the height (Step 1) to get:
Probability = 5 * 1/30 = 5/30 = 1/6.
Example Question 2: Find P(X≤10) for the above question.
This is asking you to find the probability that the random variable X is less than 10. In other words, you want to know the probability a person will gain up to ten pounds.
Step 1: Find the width of the “box”: b – a = 10 – 0 = 10.
Step 2: Multiply the width (Step 1) by the height. We already know the height is 1/30 (from example question 1), so:
10 * 1/30 = 10/30 = 1/3.
Example Question 3: Find P(20≤X≤25) for the above question. This is asking the probability of a weight gain between 20 and 25 pounds.
Step 1: Find the width of the “box”: b – a = 25 – 20 = 5.
Step 2: Multiply the width (Step 1) by the height. We already know the height is 1/30 (from example question 1), so:
5 * 1/30 = 5/30 = 1/6.
The More Formal Formula
You can solve these types of problems using the steps above, or you can us the formula for finding the probability for a continuous uniform distribution:
P(X) = d – c / b – a.
This is also sometimes written as:
P(X) = x2 – x1 / b – a.
“d” and “c” (x2 – x1)are the upper and lower bounds of the area you are trying to find.
You get exactly the same answer as if you’d followed the steps above. If formulas work for you&hellipgreat. Personally, I find it easier to visualize these problems as trying to find an area inside a rectangle. Otherwise, I’ve just got another formula to memorize.
References
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Levine, D. (2014). Even You Can Learn Statistics and Analytics: An Easy to Understand Guide to Statistics and Analytics 3rd Edition. Pearson FT Press
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.